---category_name: mediumproblem_code: ZUBGOLDproblem_name: 'B - Get The Gold'languages_supported:- C- CPP14- JAVA- PYTH- 'PYTH 3.5'max_timelimit: '3'source_sizelimit: '50000'problem_author: zubaerkhproblem_tester: nulldate_added: 10-11-2017tags:- zubaerkhtime:view_start_date: 1517085000submit_start_date: 1517085000visible_start_date: 1517085000end_date: 1735669800current: 1525198961is_direct_submittable: falselayout: problem---All submissions for this problem are available.A man in his death-bed told his lazy son that throughout his life he had worked very hard. With the money he saved he has bought gold. This gold is hidden in a forest which is represented by a 2 dimensional plane in 3 dimensional space. There are two special trees **A** and **B** in the forest. The son needs to find these trees, and a special stone **S**. He must walk from **S** to **A** along the plane representing the forest, and then take a right turn and walk the same distance (ie. walk perpendicular to **SA**), to get to a point **C**. He must then come back to **S**. Next, he should walk from **S** to **B**, take a left turn and then walk that distance again to reach the point **D**. Half way between **C** and **D** is the place where the gold is hidden.The forest is a plane defined by the points **S(x0,y0,z0)**, **A(x1,y1,z1)** and **B(x2,y2,z2)**. **S, A**, and **B** will not be collinear. You need to find the coordinates of the gold. Each input set consists of the coordinates of the points **S, A** and **B** in separate lines. It is guaranteed that the origin **O**(0,0,0) will always be above the forest surface. That is, you standing on the forest surface, if you look up, (0, 0, 0) will be in the sky.### Input- The first line contains one integer, **T**, the number of test cases. The description of each test case follows:- Three lines will be printed for each test case.- The first line will contain three space-separated numbers **x0, y0, z0**.- The second line will contain three space-separated numbers **x1, y1, z1**.- The third line will contain three space-separated numbers **x2, y2, z2**.- An empty line will be printed after each test case.- All the numbers will have two digits after the decimal point.### OutputFor each test case, print three real numbers, **x y z**, in a new line where **(x,y,z)** are the coordinates of the gold. Your answer will be considered correct if the absolute error is less than 10-6.### Constraints- 1 ≤ **T** ≤ 100000- -106 ≤ **x0, y0, z0, x1, y1, z1, x2, y2, z2** ≤ 106### Example<pre><b>Input:</b>20.00 0.00 -1.000.00 1.00 -1.002.00 1.00 -1.00-8.00 4.65 5.72-6.14 -3.43 -3.87-5.50 1.56 8.60<b>Output:</b>1.00000000 2.00000000 -1.00000000-2.29963939 -6.31303751 4.33640147</pre>### Explanation**Test case 1:** The figure below shows the scenario: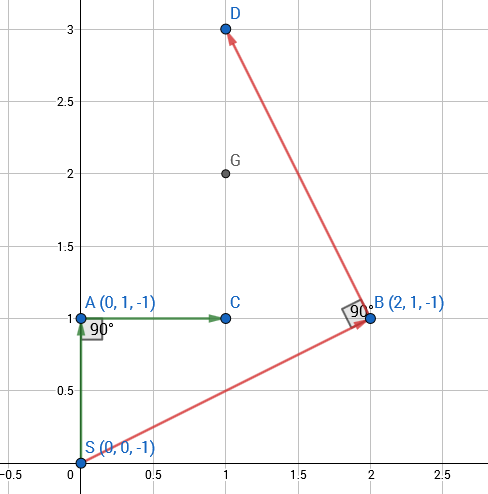The plane represented by the three input points is the plane z = -1. We have **S**(1.00, 1.00, -1.00). Going from **S** to **A**, taking a right turn, and going the same distance as **SA** will take you to the point **C**(1.00, 1.00, -1.00). Going from **S** to **B**, taking a left turn, and going the same distance as **SB** will take you to the point **D**(1.00, 3.00, -1.00). The gold is at the midpoint of segment **CD**, which is (1.00, 2.00, -1.00).