github.com/captn3m0/codechef.git

---
category_name: hard
problem_code: KILLER
problem_name: 'Painting Tree'
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 4.9.2'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYPY
    - PYTH
    - 'PYTH 3.4'
    - RUBY
    - SCALA
    - 'SCM chicken'
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '2'
source_sizelimit: '50000'
problem_author: tanuj_khattar
problem_tester: null
date_added: 8-05-2017
tags:
    - convex
    - hld
    - may17
    - tanuj_khattar
    - tree
editorial_url: 'https://discuss.codechef.com/problems/KILLER'
time:
    view_start_date: 1495099800
    submit_start_date: 1495099800
    visible_start_date: 1495099800
    end_date: 1735669800
    current: 1497589508
layout: problem
---
All submissions for this problem are available.You are given a rooted unweighted tree with **N** nodes. The nodes are numbered from 1 to **N**. Node 1 is the root. You want to paint all the vertices of this tree. There are different brushes already present in each of the nodes. You can pick the brush at one node and in a single stroke paint some consecutive nodes on the path from this node to the root, starting at this node. You want to make sure that you paint each node exactly once. Now that you have the story in mind, we will shift to a more formal description:

A path in this tree is _good_ if no two different vertices on this path are at the same distance from the root. Informally, good paths refer to paths between a node and its ancestor. A path containing a single node is good.

You need to partition all the vertices into good paths such that the total cost (describe below) is minimized. That is, you should select a set of good paths such that every node is in exactly one of the selected paths.

Depth(u) is defined to be the number of edges on the path from the root to u. So depth(1) = 0, as 1 is the root. h is the maximum depth among all the nodes.

**Cost of a path:**

Let P be a good path. Let u be the node which is farthest away from the root, on this path. The cost of this path is the (summation of **C**uw, for all w in the path) - **H**\[u\].

**C**uw is equal to (**C**\[u\]\*(h - depth(w)) + **C**\[u\]2), where **C**\[u\] is given to you.

So, put together, cost of the path = sum of ((**C**\[u\]\*(h - depth(w)) + **C**\[u\]2)) - **H**\[u\]) for all nodes w in the path.

The total cost is the sum of costs of each of the paths that you have selected. Output the minimum total cost with which you can paint all nodes.

### Input

The first line of the input contains an integer **T** denoting the number of test cases. Description of **T** test cases follow.

The first line of each test case contains one integer **N**.

The i-th of the next **N** lines contain two integers each: **H**\[i\] and **C**\[i\].

The next N-1 lines contain two integers each: u and v denoting that there is an edge between u and v.

### Output

For each test case, output one integer per line denoting the minimum total cost.

### Constraints

- 1 ≤ **T** ≤ 5
- 1 ≤ **N** ≤ 105
- 0 ≤ **C**\[i\] ≤ 105
- -1012 ≤ **H**\[i\] ≤ 1012

### Subtasks

**Subtask #1 (4 points)**

- 1 ≤ **N** ≤ 5000
- The tree is guaranteed to be a path. In particular, Node 1 is one of the end points of this path and Nodes i and i+1 are adjacent for all 1 ≤ i N

**Subtask #2 (8 points)**

- 1 ≤ **N** ≤ 5000

**Subtask #3 (48 points)**

- 1 ≤ **N** ≤ 100000
- The tree is guaranteed to be a path. In particular, Node 1 is one of the end points of this path and Nodes i and i+1 are adjacent for all 1 ≤ i N

**Subtask #4 (40 points)**

- Original constraints

### Example

<pre>
<b>Input</b>
2
3
4 5
2 3
2 2
1 2
1 3
6
1 10
1 8
10 1
1 5
9 3
8 2
1 2
1 6
2 3
2 4
4 5

<b>Output</b>
15
11
</pre>### Explanation

**Example Test case 2.**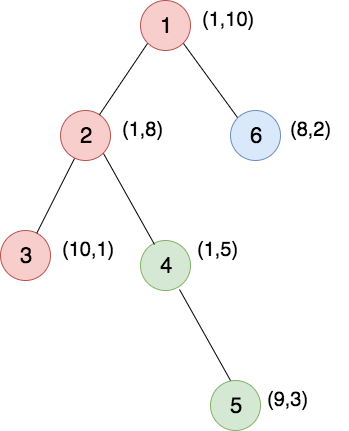

![](https://codechef_shared.s3.amazonaws.com/upfiles/killer.png)

The values in the brackets are (H,C)

The optimal solution is to paint the nodes (1,2,3) with brush 3, nodes (4,5) with brush 5 and node 6 with brush 6.

depth\[1\] = 0, depth\[2\] = 1, depth\[3\] = 2, depth\[4\] = 2, depth\[5\] = 3, depth\[6\] = 1

Hence, h = 3.

 C\[3\] \* (h - depth\[3\]) + C\[3\]^2 = 1 \* (3 - 2) + 1^2 = 2 C32 = C\[3\] \* (h - depth\[2\]) + C\[3\]^2 = 1 \* (3 - 1) + 1^2 = 3

C31 = C\[3\] \* (h - depth\[1\]) + C\[3\]^2 = 1 \* (3 - 0) + 1^2 = 4

C55 = C\[5\] \* (h - depth\[5\]) + C\[5\]^2 = 3 \* (3 - 3) + 3^2 = 9

C54 = C\[5\] \* (h - depth\[4\]) + C\[5\]^2 = 3 \* (3 - 2) + 3^2 = 12

C66 = C\[6\] \* (h - depth\[6\]) + C\[6\]^2 = 2 \* (3 - 1) + 2^2 = 8

**Total Cost** = 2 + 3 + 4 + 9 + 12 + 8 - H\[3\] - H\[5\] - H\[6\] = 38 - 10 - 9 - 8 = 11