github.com/captn3m0/codechef.git

---
category_name: hard
problem_code: LUCASTH
problem_name: 'Lucas Theorem'
languages_supported:
    - C
    - CPP14
    - JAVA
    - PYTH
    - 'PYTH 3.5'
    - PYPY
    - CS2
    - 'PAS fpc'
    - 'PAS gpc'
    - RUBY
    - PHP
    - GO
    - NODEJS
    - HASK
    - rust
    - SCALA
    - swift
    - D
    - PERL
    - FORT
    - WSPC
    - ADA
    - CAML
    - ICK
    - BF
    - ASM
    - CLPS
    - PRLG
    - ICON
    - 'SCM qobi'
    - PIKE
    - ST
    - NICE
    - LUA
    - BASH
    - NEM
    - 'LISP sbcl'
    - 'LISP clisp'
    - 'SCM guile'
    - JS
    - ERL
    - TCL
    - kotlin
    - PERL6
    - TEXT
    - 'SCM chicken'
    - CLOJ
    - COB
    - FS
max_timelimit: '4'
source_sizelimit: '50000'
problem_author: yzl427
problem_tester: r_64
date_added: 24-11-2017
tags:
    - divide
    - feb18
    - fft
    - lucas
    - math
    - yzl427
editorial_url: 'https://discuss.codechef.com/problems/LUCASTH'
time:
    view_start_date: 1518427800
    submit_start_date: 1518427800
    visible_start_date: 1518427800
    end_date: 1735669800
    current: 1525454466
is_direct_submittable: false
layout: problem
---
All submissions for this problem are available.### Read problems statements in [Mandarin chinese](http://www.codechef.com/download/translated/FEB18/mandarin/LUCASTH.pdf), [Russian](http://www.codechef.com/download/translated/FEB18/russian/LUCASTH.pdf) and [Vietnamese](http://www.codechef.com/download/translated/FEB18/vietnamese/LUCASTH.pdf) as well.

Chef is tired of solving boring math problems by hand. One of these problems is summing up the products of elements from each **k**-subset of the set **\[n\]**. Here, a **k**-subset is a subset containing exactly **k** elements and **\[n\]** refers to the set which contains all integers between **1** and **n** (inclusive). More formally: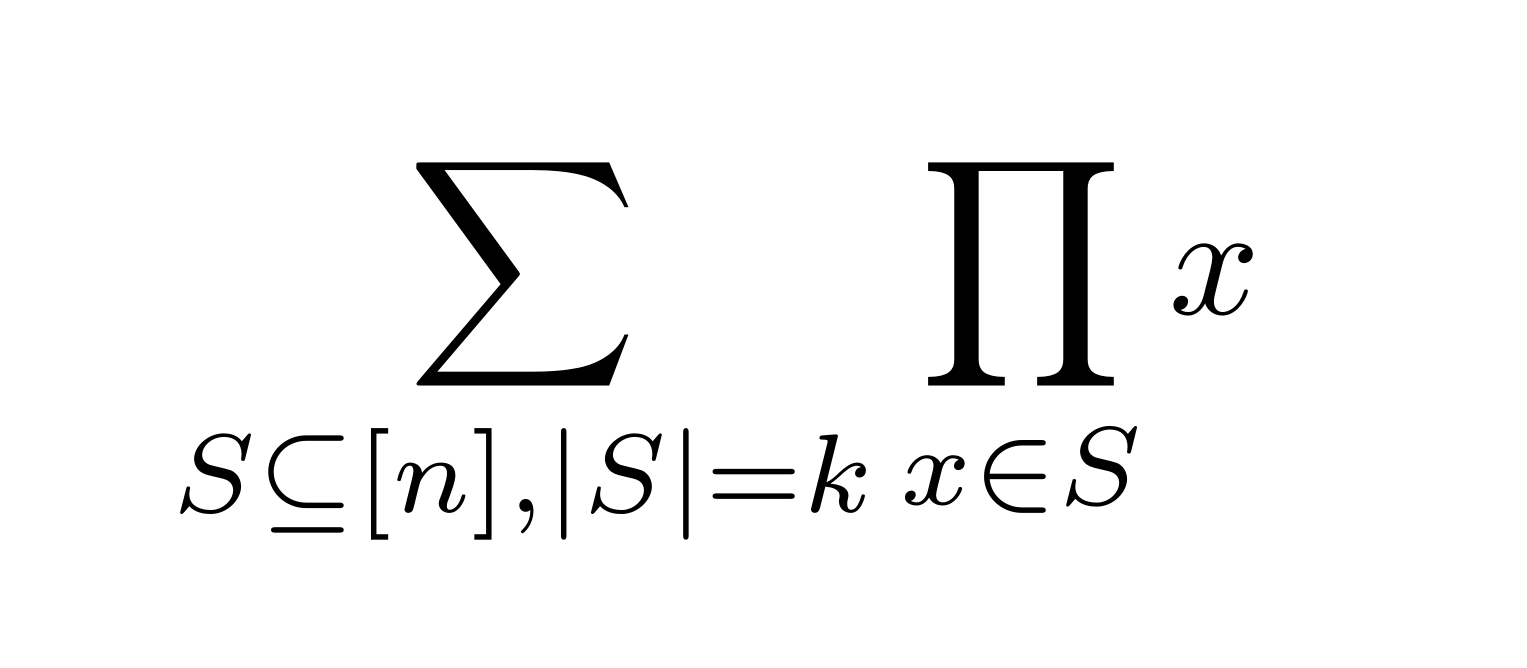

![](https://raw.githubusercontent.com/Lucas110550/ProblemImages/master/lucasth.png)Let’s denote this number by **f**(**n**, **k**). Note that **f**(**n**, 0) = 1.

Since calculating **f(n, k)** is too boring, Chef wants to know how the divisibility of **f(n, k)** by a given prime **p** depends on **k**. Specifically, for a fixed **n**, you should compute the number of ways to select **k** (0 ≤ **k** ≤ **n**) so that **f**(**n**, **k**) isn't divisible by **p**. After a while of thinking, Chef realized there might be too many ways to do that. Therefore, you should compute this number modulo **109+7**.

### Input

- The first line of the input contains a single integer **T** denoting the number of test cases. The description of **T** test cases follows.
- The first and only line of each test case contains two space-separated integers **n** and **p**.

### Output

For each test case, print a single line containing one number — the number of ways to select **k**, modulo 109+7.

### Constraints

- 1 ≤ **T** ≤ 4
- 1 ≤ **n** < 10501
- **n** does not contain leading zeroes
- 2 ≤ **p** ≤ 100,000
- **p** is prime

### Subtasks

**Subtask #1 (10 points):** **n** ≤ 5,000

**Subtask #2 (40 points):** **n** ≤ 100,000

**Subtask #3 (50 points):** original constraints

### Example

<pre><b>Input:</b>

1
4 2

<b>Output:</b>

2
</pre>### Explanation

**Example case 1:** The values of **f**(4, **k**) are as follows:

- **f**(4, 0) = 1
- **f**(4, 1) = 1+2+3+4 = 10
- **f**(4, 2) = 1·2+2·3+3·4+4·1+1·3+2·4 = 35
- **f**(4, 3) = 1·2·3+2·3·4+1·3·4+1·2·4 = 50
- **f**(4, 4) = 1·2·3·4 = 24

Only **k** = 0 and **k** = 2 give numbers indivisible by **p** = 2, so the answer is 2.