github.com/captn3m0/codechef.git

---
category_name: hard
problem_code: BOUNCE
problem_name: 'Advanced Cooking Machine'
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 4.9.2'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYPY
    - PYTH
    - 'PYTH 3.4'
    - RUBY
    - SCALA
    - 'SCM chicken'
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '7'
source_sizelimit: '50000'
problem_author: kevinsogo
problem_tester: null
date_added: 21-11-2016
tags:
    - kevinsogo
time:
    view_start_date: 1481535000
    submit_start_date: 1481535000
    visible_start_date: 1481535000
    end_date: 1735669800
    current: 1493556627
layout: problem
---
All submissions for this problem are available.###  Read problems statements in [Mandarin Chinese](http://www.codechef.com/download/translated/DEC16/mandarin/BOUNCE.pdf), [Russian](http://www.codechef.com/download/translated/DEC16/russian/BOUNCE.pdf) and [Vietnamese](http://www.codechef.com/download/translated/DEC16/vietnamese/BOUNCE.pdf) as well.

The most advanced cooking machine is in town! It's called the **Advanced Cooking Machine**, or **ACM**. The company that sells them is the **ICPC**. (You can come up with an acronym yourself.)

Each ACM is rectangular in shape (when viewed from the top) with integer dimensions. No ACM is square-shaped.

The ACM is quite unique in its cooking method. When it starts, a magical beam of "cooking laser" is fired from the bottom-left corner at an angle of 45 degrees from the side. The laser beam passes through food completely and cooks them. However, when the beam hits one of the sides, it bounces in such a way that the angle remains 45 degrees. See the following image for an illustration: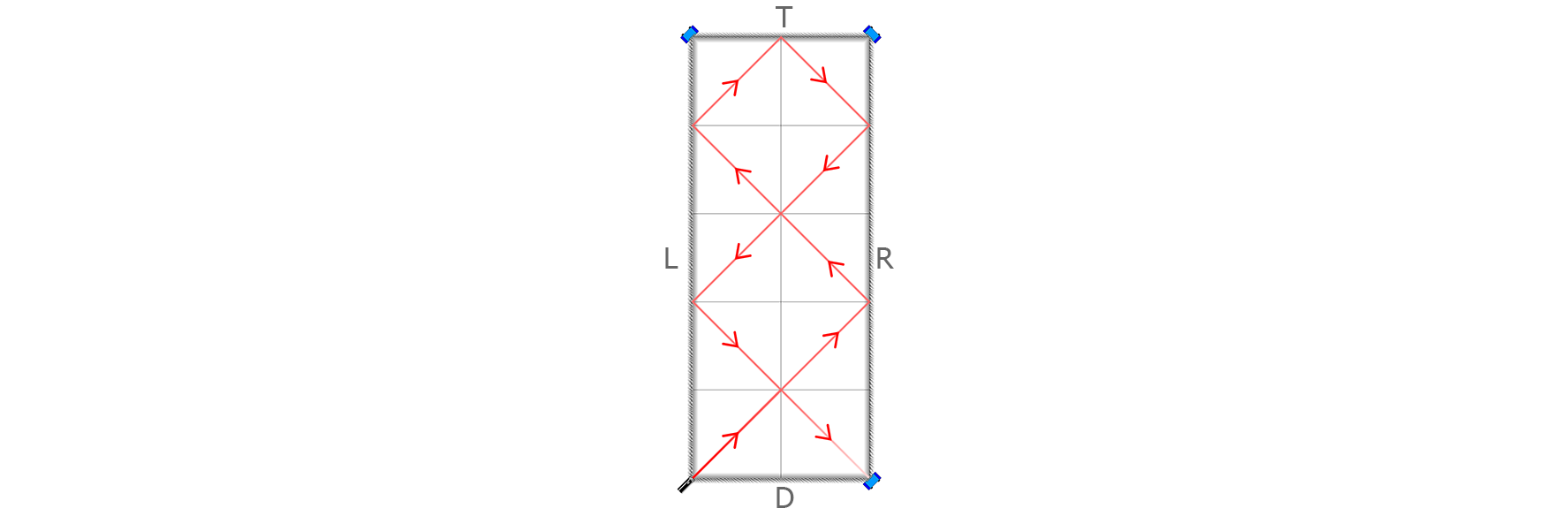

![](https://codechef_shared.s3.amazonaws.com/download/upload/bounce.png)The cooking ends when the beam hits any of the corners, in which case it is absorbed by the machine.

In addition, the four sides of an ACM are fitted with detectors, one for each side. These are used to keep track of the ACM's cooking performance. As the beam hits a side, the corresponding detector activates and then prints a single letter to the ACM's display. The top, left, bottom and right detectors output T, L, D and R respectively. Thus, when the cooking ends, a string of letters TLDR will be printed on the screen. For example, the ACM in the image above prints the string RLTRL.

Naturally, this string will always be the same for a particular ACM; in other words it is only dependent on the dimensions **R × C**. Let's call this string the **signature string** of the ACM, and denote it as **f(R, C)**.

And since a longer signature string means more thorough cooking, the ICPC has decided to set the price of an ACM to be the length of the signature string, in dollars! In other words, the cost of the **R × C** ACM is **|f(R, C)|** dollars.

Chef, in keeping up with the times, has bought an ACM with dimensions **R × C**. Chef loved the ACM very much! Unfortunately, he loved it too much, that the ACM broke due to overuse. This made Chef very upset, and so he's seeking a replacement.

Chef wants an exact replica of his ACM, but he doesn't remember **R × C**! All he remembers are the following:

1. **1 ≤ R ≤ N** and **1 ≤ C ≤ N**.
2. **f(R, C)** starts with the string **S**.

Chef will do anything just to get his original ACM back, even if it means spending more than necessary. He decided to buy all ACMs whose dimensions **R × C** satisfy the above. Your problem is now to compute Chef's total spendings, i.e., find the total cost of all distinct ACMs satisfying the two requirements above.

_Note:_ Two ACMs with the same dimensions are identical, but ACMs cannot be rotated, i.e., **R × C** is different from **C × R**.

### Input

The first line of input contains an integer **T** denoting the number of test cases. The description of **T** test cases follows.

The first line of each test case contains two integer **N** and **|S|** separated by a space.

The second line contains the string **S**.

### Output

For each test case, output a single line containing the answer. Since the answer can be very large, only output it modulo **109 + 7**.

### Constraints

- **1 ≤ |S| ≤ 106**
- The sum of the **|S|** in a single file is  **≤ 106**
- **S** is a string consisting of the letters TLDR.

### Subtasks

**Subtask #1 (10 points):**- **1** ≤ **T** ≤ **500**
- **4** ≤ **N** ≤ **500**
- **1 ≤ |S| ≤ 103**

**Subtask #2 (25 points):**- **1** ≤ **T** ≤ **200**
- **4** ≤ **N** ≤ **105**

**Subtask #3 (65 points):**- **1** ≤ **T** ≤ **5**
- **4** ≤ **N** ≤ **1010**

### Example

<pre><b>Input:</b>
<tt>2
5 4
RLTR
4 4
RLTR</tt>
<b>Output:</b>
<tt>5
0</tt>
</pre>### Explanation

In the first test case, there is only one ACM satisfying the requirements, and that is the ACM with dimensions **5 × 2**. **f(5,2)** = RLTRL has length **5**, so the total cost is **5**.

In the second test case, no ACMs satisfy the requirements, so the total cost is 0.