github.com/captn3m0/codechef.git

---
category_name: medium
problem_code: MANCBST
problem_name: 'Chef Counts Semi-BSTs'
languages_supported:
    - C
    - CPP14
    - JAVA
    - 'PYTH 3.5'
    - CS2
    - 'PAS fpc'
    - 'PAS gpc'
    - GO
    - NODEJS
    - HASK
    - D
    - PERL
    - FORT
    - ADA
    - CAML
    - ICK
    - BF
    - ASM
    - CLPS
    - ICON
    - NICE
    - LUA
    - BASH
    - NEM
    - 'LISP sbcl'
    - 'LISP clisp'
    - JS
    - ERL
    - kotlin
    - PERL6
    - CLOJ
    - COB
    - FS
max_timelimit: '1.5'
source_sizelimit: '50000'
problem_author: satyaki3794
problem_tester: null
date_added: 30-11-2017
tags:
    - acm17chn
    - chn17rol
    - fft
    - med
    - satyaki3794
editorial_url: 'https://discuss.codechef.com/problems/MANCBST'
time:
    view_start_date: 1515357000
    submit_start_date: 1515357000
    visible_start_date: 1515357000
    end_date: 1735669800
    current: 1525454447
is_direct_submittable: false
layout: problem
---
All submissions for this problem are available.Everyone has heard of binary search trees or BSTs. A BST is a rooted tree, such that the root has atmost two children. The subtree rooted at each of root's children should be valid BSTs. All the values in the left subtree should be smaller than the root and all the values in the right subtree should be larger than the root.

However, there's a new data structure in town called semi-BST. Formally, a semi-BST is a tree with **N** nodes which satisfies the following conditions:

- Each node contains a distinct value.
- The root has at most two children.
- The right subtree of the root (if it exists) is a valid semi-BST.
- The left subtree of the root (if it exists) is any unordered rooted tree. That is, the children of a vertex are not ordered, and hence no concept of left or right child.
- The BST property for the root is maintained, i.e. all the values in the left subtree of the root are lesser than that of the root and all the values in the right subtree of the root are greater than that of the root.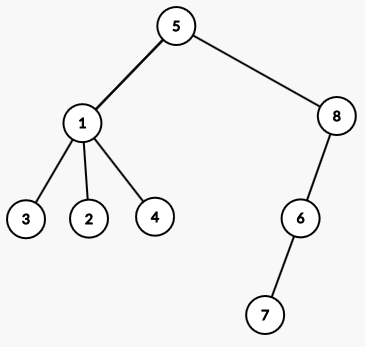

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17CHN/MANCBST.png)For example, let us show that tree shown above is a semi-BST. The root of the tree is 5. All the elements in the left subtree are smaller than 5 and all the elements in the right subtree are greater than 5.

Now, all we need to show is that the right subtree is a valid semi-BST:

We are now considering the subtree rooted at 8, and hence the current root is 8. All the elements in the left subtree are smaller than 8 and all the elements in the right subtree (which doesn't exist) are greater than 8. Hence the subtree rooted at 8 is a valid semi-BST. And hence the entire tree, rooted at 5 is a valid semi-BST.

Given **N**, find the number of semi-BSTs having exactly **N** nodes, and such that all the **N** values in the nodes are from {1, 2, ..., **N**}. Output the answer modulo 663224321.

### Input

- The first line of the input contains a single integer **T** denoting the number of test cases. The description of **T** test cases follows.
- The first and only line of each test case contains a single integer **N** denoting the number of nodes.

### Output

For each test case, print a single line containing one integer — the number of semi-BSTs modulo 663224321.

### Constraints

- 1 ≤ **T** ≤ 100000
- 1 ≤ **N** ≤ 100000

### Example 1

<pre><b>Input:</b>
4
1
2
3
4

<b>Output:</b>
1
2
5
18
</pre>