---category_name: hardproblem_code: QGRIDproblem_name: 'Querying on a Grid'languages_supported:- ADA- ASM- BASH- BF- C- 'C99 strict'- CAML- CLOJ- CLPS- 'CPP 4.3.2'- 'CPP 6.3'- CPP14- CS2- D- ERL- FORT- FS- GO- HASK- ICK- ICON- JAVA- JS- kotlin- 'LISP clisp'- 'LISP sbcl'- LUA- NEM- NICE- NODEJS- 'PAS fpc'- 'PAS gpc'- PERL- PERL6- PHP- PIKE- PRLG- PYPY- PYTH- 'PYTH 3.5'- RUBY- rust- SCALA- 'SCM chicken'- 'SCM guile'- 'SCM qobi'- ST- swift- TCL- TEXT- WSPCmax_timelimit: '7'source_sizelimit: '50000'problem_author: r_64problem_tester: jingbo_admdate_added: 6-08-2017tags:- divide- hard- r_64- sept17- shortesteditorial_url: 'https://discuss.codechef.com/problems/QGRID'time:view_start_date: 1505122200submit_start_date: 1505122200visible_start_date: 1505122200end_date: 1735669800current: 1514816033layout: problem---All submissions for this problem are available.### Read problems statements in [mandarin chinese](http://www.codechef.com/download/translated/SEPT17/mandarin/QGRID.pdf), [russian](http://www.codechef.com/download/translated/SEPT17/russian/QGRID.pdf) and [vietnamese](http://www.codechef.com/download/translated/SEPT17/vietnamese/QGRID.pdf) as well.Chef is helping out at a volunteering center for teaching. A child comes to Chef with a problem that he is not able to solve and asks Chef for his help. The problem is the following:Consider an **M × N** grid graph. The vertices in the grid graph are identified by its row and column number, i.e., for a vertex there are two numbers **(i,j)** associated with it, where **1 ≤ i ≤ M** is its row, and **1 ≤ j ≤ N** is its column. There are two types of edges in a grid graph(note that all edges are bidirectional) :- When **i < M**, there is an edge of weight **down(i, j)** connecting **(i, j)** and **(i+1, j)**;- When **j < N**, there is an edge of weight **right(i, j)** connecting **(i, j)** and **(i, j+1)**.Initially, every vertex has a weight of zero.Define the length of a path to be the sum of weights of all the edges in this path. The shortest path between **(i1, j1)** and **(i2, j2)** is the path with the minimum length. Of course, the weights associated with vertices doesn't influence shortest paths at all.The task in the problem is to process the following 2 types of queries on this graph efficiently :- **i1** **j1** **i2** **j2** **c** : add **c** to the weights of all vertices in the shortest path between **(i1, j1)** and **(i2, j2)**.- **i** **j** : return the weight of vertex **(i, j)**.Chef is confused with the problem but he wants to help the child. Can you help Chef with this problem?### InputThe first line contains three integers **M, N, Q**. **M** and **N** denotes the graph's size; **Q** denotes the number of queries.Next **M - 1** lines, each line contains **N** numbers. The **j**-th number in the **i**-th line in this part(i.e., the **(i + 1)**-th line in total) denotes **down(i, j)**.Next **M** lines, each line contains **N - 1** numbers. The **j**-th number in the **i**-th line in this part(i.e., the **(i + M)**-th line in total) denotes **right(i, j)**.Next **Q** lines, each line contains 3 or 6 numbers, denoting a query.### OutputFor each query of type 2, output the weight of required vertex.### Constraints- **1** ≤ **M** ≤ **3**- **1** ≤ **N** ≤ **105**- **1** ≤ **Q** ≤ **105**- **1** ≤ **down(i,j), right(i,j)** ≤ **1012**- In type 1 query :- **1** ≤ **i1, i2** ≤ **M**- **1** ≤ **j1, j2** ≤ **N**- **1** ≤ **c** ≤ **1013**- The shortest path between **(i1, j1)** and **(i2, j2)** is **unique**.- In type 2 query :- **1** ≤ **i** ≤ **M**- **1** ≤ **j** ≤ **N**### Subtasks- **Subtask #1 (6 points)**: **N, Q ≤ 103**- **Subtask #2: (11 points)**: **M = 1**.- **Subtask #3: (30 points)**: **M = 2**.- **Subtask #4: (24 points)**:- **down(i,j)** and **right(i,j)** are uniformly randomly generated from **\[1,3 × 1010\]**.- Queries are also randomly generated.- There is only one test file for this subtask.- **Subtask #5: (29 points):**: Original Constraints### Example<pre><b>Input:</b>3 3 111 1 52 10 61 41 136 51 2 2 3 3 11 2 2 1 3 22 1 12 1 22 1 32 2 12 2 22 2 32 3 12 3 22 3 3<b>Output:</b>022130111</pre>### Explanation**Example case 1.** See picture below.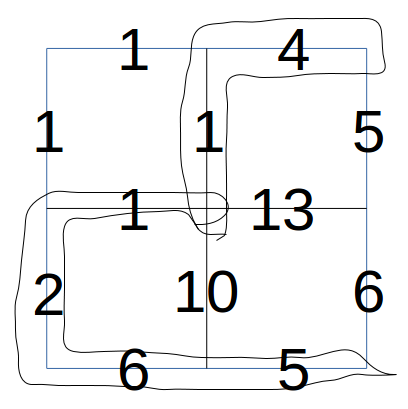The shortest path between (2,2) and (3,3) is (2,2)->(2,1)->(3,1)->(3,2)->(3,3). We add 1 to these 5 vertices.The shortest path between (2,2) and (1,3) is (2,2)->(1,2)->(1,3). We add 2 to these 3 vertices.Note that the shortest path between (1,1) and (2,2) is not unique. However, the queried paths are (2,2)-(3,3) and (2,2)-(1,3), and the shortest paths of these pairs of points are unique, so this data is valid.