github.com/captn3m0/codechef.git

---
category_name: easy
problem_code: TALETRI
problem_name: 'A Tale of Two Right Angled Triangles'
languages_supported:
    - C
    - CPP14
    - JAVA
    - PYTH
    - 'PYTH 3.5'
max_timelimit: '2'
source_sizelimit: '50000'
problem_author: admin2
problem_tester: null
date_added: 19-12-2017
tags:
    - admin2
    - easy
    - gwr17rol
time:
    view_start_date: 1516482000
    submit_start_date: 1516482000
    visible_start_date: 1516482000
    end_date: 1735669800
    current: 1525454371
is_direct_submittable: false
layout: problem
---
All submissions for this problem are available.You are given two right angled triangles. You are given their side lengths. The first triangle is ABC, where side AB is the hypotenuse. Length of AB is **c**, that of AC is **b**, and that of BC is **a**. Similarly, the second triangle is DEF, where DE is the hypotenuse. Length of DE is **f**, that of DF is **e**, and that of EF is **d**.

First we define _minimum area enclosing axis-parallel rectangle_ of some figures. It will be a rectangle which is axis parallel (i.e. each of its sides should be parallel to x or y axis) that encloses all the figures and has the minimum possible area. By enclosing, we mean that all the figures should be inside the rectangle.

You have to find a set of coordinates to assign to the points A, B, C, D, E, F such that the _minimum area enclosing axis-parallel rectangle_ of the two triangles has sides **L** and **R**, i.e. one side is of length **L**, and the other is of length **R**. Also, each of the sides AC, BC, DF, EF should be parallel to either x or y axis. If it is not possible to assign the coordinates, output -1.

### Input

- The first line of the input contains a single integer **T** denoting the number of test cases. The description of **T** test cases follows.
- The only line of each test case contains eight space separated integers denoting the lengths **a, b, c, d, e, f, L, R**.

### Output

For each test case, either output -1 if it is impossible to assign the coordinates. Otherwise, output six lines each containing two space separated integers corresponding to the coordinates of points A, B, C, D, E, F in that order. You can output any possible coordinates that have their absolute values less than or equal to 109.

### Constraints

- 1 ≤ **T** ≤ 105
- 1 ≤ **a, b, c, d, e, f, L, R** ≤ 108
- **a2 + b2 = c2**
- **d2 + e2 = f2**

### Example

<pre>
<b>Input</b>
2
3 4 5 3 4 5 4 4
3 4 5 3 4 5 2 4

<b>Output</b>
2 5
5 1
2 1
2 4
6 1
6 4
-1
</pre>### Explanation

**Testcase 1**: The output corresponds to the image shown below: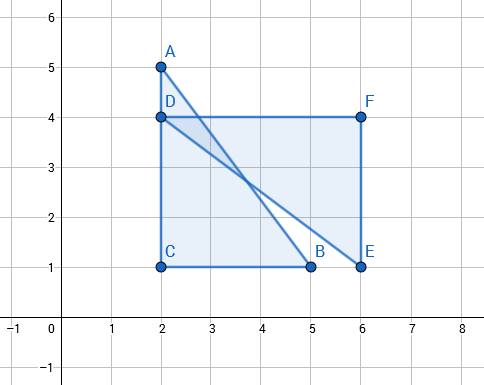

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17GWR/TALETRI-1.png)

Notice that all the 6 side lengths are maintained, and the sides AC, BC, DF, EF are all axis-parallel. The _minimum area enclosing axis-parallel rectangle_ of these two triangles is shown in the next image: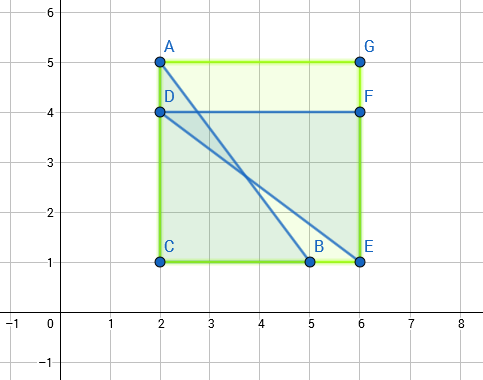

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17GWR/TALETRI-2.png)

Notice that this is a rectangle with side lengths 4 and 4, just as we wanted. Hence this is a valid output.