github.com/captn3m0/codechef.git

---
category_name: easy
problem_code: PETERSEN
problem_name: 'Petersen Graph'
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 4.9.2'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYTH
    - 'PYTH 3.4'
    - RUBY
    - SCALA
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '1'
source_sizelimit: '50000'
problem_author: kostya_by
problem_tester: null
date_added: 25-10-2014
tags:
    - bfs
    - cook52
    - graphs
    - kostya_by
    - simple
    - traversal
editorial_url: 'http://discuss.codechef.com/problems/PETERSEN'
time:
    view_start_date: 1416767862
    submit_start_date: 1416767862
    visible_start_date: 1416767794
    end_date: 1735669800
    current: 1493558173
layout: problem
---
All submissions for this problem are available.###  Read problems statements in [Mandarin Chinese](http://www.codechef.com/download/translated/COOK52/mandarin/PETERSEN.pdf) and [Russian](http://www.codechef.com/download/translated/COOK52/russian/PETERSEN.pdf) as well.

 The following graph **G** is called a [Petersen graph](http://en.wikipedia.org/wiki/Petersen_graph) and its vertices have been numbered from 0 to **9**. Some letters have also been assigned to vertices of **G**, as can be seen from the following picture: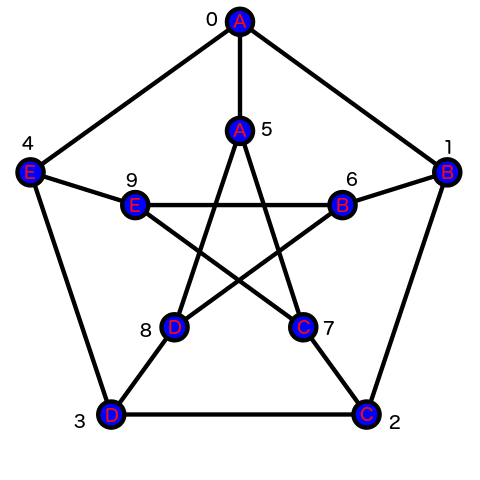

 ![](//www.codechef.com//download/Petersen1tinysvg.png)

 Let's consider a walk **W** in graph **G**, which consists of **L** vertices **W1**, **W2**, ..., **WL**, such that **Wi** is connected with **Wi + 1** for 1 ≤ **i** < **L**. A string **S** of **L** letters **'A'-'E'** is realized by walk **W** if the sequence of letters written along **W** is equal to **S**. Vertices can be visited multiple times while walking along **W**.

For example, **S** = **'ABBECCD'** is realized by **W** = (0, 1, 6, 9, 7, 2, 3).

Your task is to determine whether there is a walk **W** which realizes a given string **S** in graph **G**, and if so, find the lexicographically least such walk.

### Input

 The first line of the input contains one integer **T** denoting the number of testcases to process.

 The only line of each testcase contains one string **S**. It is guaranteed that **S** only consists of symbols **'A'-'E'**.

### Output

 The output should contain exactly **T** lines, one line per each testcase in the order of their appearance. For each testcase, if there is no walk **W** which realizes **S**, then output **-1**. Otherwise, you should output the least lexicographical walk **W** which realizes **S**. Since all of the vertices are numbered from 0 to **9**, then it can be encoded as a string consisting of symbols **'0'-'9'** (see the "Examples" section for more details).

### Constraints

1 ≤ **T** ≤ 8;

1 ≤ **|S|** ≤ 100000(105).

### Examples

<pre><b>Input:</b>
2
AAB
AABE

<b>Output:</b>
501
-1
</pre>