github.com/captn3m0/codechef.git

---
category_name: medium
problem_code: CHEFDIV
problem_name: 'Chef and Divisor Tree'
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 4.9.2'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYPY
    - PYTH
    - 'PYTH 3.4'
    - RUBY
    - SCALA
    - 'SCM chicken'
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '1'
source_sizelimit: '50000'
problem_author: saluja123
problem_tester: null
date_added: 23-02-2017
tags:
    - april17
    - saluja123
editorial_url: 'https://discuss.codechef.com/problems/CHEFDIV'
time:
    view_start_date: 1492421400
    submit_start_date: 1492421400
    visible_start_date: 1492421400
    end_date: 1735669800
    current: 1497284426
layout: problem
---
All submissions for this problem are available.###  Read problems statements in [Mandarin Chinese](http://www.codechef.com/download/translated/APRIL17/mandarin/CHEFDIV.pdf), [Russian](http://www.codechef.com/download/translated/APRIL17/russian/CHEFDIV.pdf) and [Vietnamese](http://www.codechef.com/download/translated/APRIL17/vietnamese/CHEFDIV.pdf) as well.

Chef has defined a new type of rooted tree - _divisor tree_. In this tree, every node has a positive integer written on it. It follows some rules:

- The root can have any positive integer written on it.
- Suppose a node has the integer A written on it, and suppose A has k [proper divisors](http://mathworld.wolfram.com/ProperDivisor.html). \[Note: Proper divisors of an integer are all its divisors except the integer itself. 1 has no proper divisor\] Then this node will have exactly k child nodes, and each of A's proper divisors will be written on exactly one of the child nodes. For example, a node with number 12 written on it would have children with the numbers 1, 2, 3, 4, and 6 written on them.

You can observe that the nodes have 1 written on them, if and only if, they are leaves.

The score of a path in this tree is defined as the sum of degrees of all of the nodes in the path. The Score of the tree is defined as the maximum score of a path **from the root to one of the leaves**.

You are given two integers **A, B**. You want to find the sum of Scores of all the _divisor trees_ which have n written on their root, where **A** ≤ n ≤ **B**.

### Input

The only line of the input contains two space separated integers **A** and **B** respectively.

### **Output**

Output a single integer corresponding to the answer of the problem.

### Constraints

- 1 ≤  **A** ≤ **B** ≤ 1012
- **B - A**  5

### Subtasks

**Subtask #1 (10 points):**

- 1 ≤  **A** ≤ **B** ≤ 50

**Subtask #2 (25 points):**

- 1 ≤ **A** ≤ **B** ≤ 106
- **B - A** 5

**Subtask #3 (25 points):**

- **A = B**

**Subtask #4 (40 points):**

- Original constraints.
 
### Example

<pre><b>Input 1:</b>
11 12

<b>Output 1:</b>
14
</pre><pre><b>Input 2:</b>
932451 935212

<b>Output 2:</b>
101245
</pre>###   **Explanation**  

**Input 1.**

Here we have, **A** = 11 and **B** = 12.

The Score of the _divisor tree_ which has 12 written on its root is 12. This because the path 12 -> 6 -> 3 -> 1 (look at the figure below) has sum of the degrees of all nodes in it = 5 + 4 + 2 + 1 = 12. This is the maximum score of a path among all paths from root to the leaves. Hence, the Score of this tree is 12. 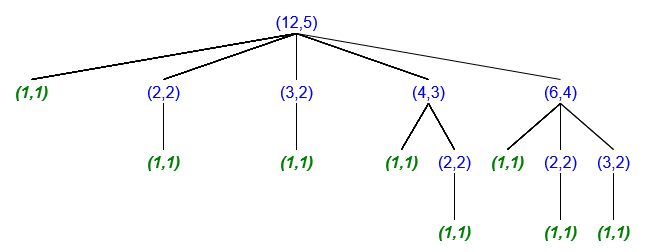![](https://codechef_shared.s3.amazonaws.com/download/upload/APRIL17/chefdiv.png)

Note that in the figure, the nodes are denoted by (value written on it, degree of node), and the leaves are marked green.

You can find that the score of divisor tree which has 11 written on its root is 2.

Hence, answer will be 12 + 2 = 14.