github.com/captn3m0/codechef.git

---
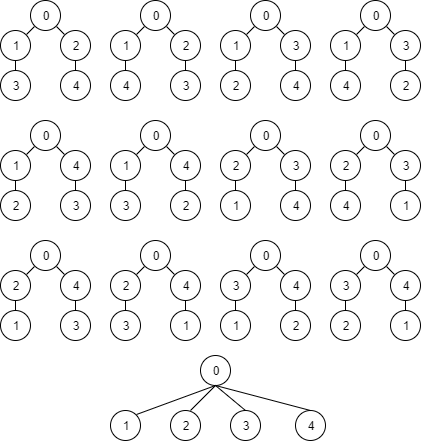
category_name: hard
problem_code: ZUBHTREE
problem_name: 'F - Huge Number of Trees'
languages_supported:
    - C
    - CPP14
    - JAVA
    - PYTH
    - 'PYTH 3.5'
max_timelimit: '2'
source_sizelimit: '50000'
problem_author: zubaerkh
problem_tester: null
date_added: 12-11-2017
tags:
    - zubaerkh
time:
    view_start_date: 1517085000
    submit_start_date: 1517085000
    visible_start_date: 1517085000
    end_date: 1735669800
    current: 1525454409
is_direct_submittable: false
layout: problem
---
All submissions for this problem are available.Hermione needs to solve a tough homework problem in Arithmancy class. Professor Vector was discussing trees for some time and now he gives the problem: Say, there are **n** + 1 nodes numbered 0, 1, 2, ..., **n**. Node 0 is always the root of the tree. How many different trees can be formed using the remaining **n** nodes so that all leaves have the same _depth_ and the _degree_ of each non-leaf node is at least **d**? Here, _depth_ of a node **u** is the number of edges we need to traverse from the root (Node 0) to reach **u**. A tree is different from another tree if there exists at least one pair of nodes **(u, v)** for which an edge between **u** and **v** is present in one tree, but absent in the other one. Hermione wants your help to write a program to solve this problem.

Note that by _degree_, we mean the total number of neighbors, not just the number of children.

### Input

- The first line of the input contains a positive integer, **T** which denotes the number of test cases.
- For each case, there is one line of input containing two integers: **n** and the minimum degree of each non-leaf node, **d**.

### Output

For each test case, print "Case i: ", and then the answer (mod 109 + 7), where i is the testcase number, 1-indexed.

### Constraints

- 1 ≤ **T** ≤ 2000
- 2 ≤ **n** ≤ 500
- 2 ≤ **d** ≤ 10

### Example

<pre><b>Input:</b>
3
2 2
3 2
4 2

<b>Output:</b>
Case 1: 1
Case 2: 1
Case 3: 13
</pre>### Explanation

**Testcase 1:** The only valid tree is shown below: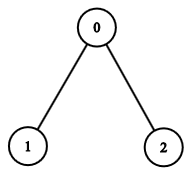

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17KOL/ZUBHTREE/ZUBHTREE.1.png)

**Testcase 2:** The only valid tree is shown below:

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17KOL/ZUBHTREE/ZUBHTREE.2.png)

**Testcase 3:** The 13 different valid trees are as shown below:

![](https://codechef_shared.s3.amazonaws.com/download/upload/ACM17KOL/ZUBHTREE/ZUBHTREE.3.png)