github.com/captn3m0/codechef.git

---
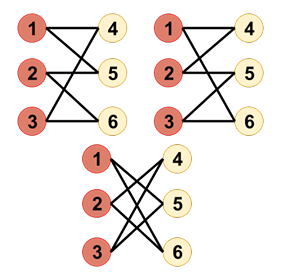
category_name: medium
problem_code: BCYCLES
problem_name: BiCycles
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 6.3'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYPY
    - PYTH
    - 'PYTH 3.5'
    - RUBY
    - SCALA
    - 'SCM chicken'
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '3.5'
source_sizelimit: '50000'
problem_author: alei
problem_tester: null
date_added: 26-06-2017
tags:
    - alei
time:
    view_start_date: 1498908900
    submit_start_date: 1498908900
    visible_start_date: 1498908900
    end_date: 1735669800
    current: 1514816015
layout: problem
---
All submissions for this problem are available.###  Read problems statements in [Mandarin Chinese](http://www.codechef.com/download/translated/SNCKFL17/mandarin/BCYCLES.pdf), [Russian](http://www.codechef.com/download/translated/SNCKFL17/russian/BCYCLES.pdf) and [Vietnamese](http://www.codechef.com/download/translated/SNCKFL17/vietnamese/BCYCLES.pdf) as well.

Given a bipartite graph of **N** vertices in which every vertex has degree exactly 3, find a set of **distinct** simple cycles such that every edge belongs to exactly two cycles. The vertices are numbered from 1 to **N**. For the given constraints, it can be shown that such a set of cycles always exists.

A simple cycle of length k (k must be at least 3) in the graph is a sequence of vertices v1, v2, .., vk, such that vi ≠ vj if i ≠ j, and such that there exist edges between vertex vi and vi + 1 for i k and v1.

### Input

The first line of the input contains an integer **T**, denoting the number of test cases.

The first line of each test case contains one integer **N**, denoting the number of vertices in the graph.

Each of the next 3 × **N**/2 lines contains two integers **u**, **v**, denoting an edge of the graph.

### Output

For each test case describe any valid set of cycles. First print **C**, the number of cycles.

In the next **C** lines describe one cycle per line: the i-th line should contain an integer **ki**, denoting the number of vertices in the i-th cycle, followed by **ki** space separated integers, which should be the sequence of vertices of the cycle in order.

### Constraints

- 6 ≤ **N** ≤ 105
- **N** is an even integer
- 1 ≤ **u**, **v** ≤ **N**
- The sum of **N** over all test cases is at most 5 × 105
- The graph is guaranteed to be bipartite, and every vertex will have degree exactly 3
- The graph will not have multi-edges or loops

### Example

<pre><b>Input:</b>
1
6
1 4
1 5
1 6
2 4
2 5
2 6
3 4
3 5
3 6

<b>Output:</b>
3
6 3 6 2 5 1 4
6 3 5 2 4 1 6
6 3 5 1 6 2 4
</pre>### Explanation

The following image depicts the three cycles in the output of the sample case. Note that for every edge in the original graph, there are two cycles that contain it.

![](https://codechef_shared.s3.amazonaws.com/download/upload/SNCKFL17/1.png)