github.com/captn3m0/codechef.git

---
category_name: hard
problem_code: MULDIG
problem_name: 'Multiplication Program'
languages_supported:
    - ADA
    - ASM
    - BASH
    - BF
    - C
    - 'C99 strict'
    - CAML
    - CLOJ
    - CLPS
    - 'CPP 4.3.2'
    - 'CPP 6.3'
    - CPP14
    - CS2
    - D
    - ERL
    - FORT
    - FS
    - GO
    - HASK
    - ICK
    - ICON
    - JAVA
    - JS
    - 'LISP clisp'
    - 'LISP sbcl'
    - LUA
    - NEM
    - NICE
    - NODEJS
    - 'PAS fpc'
    - 'PAS gpc'
    - PERL
    - PERL6
    - PHP
    - PIKE
    - PRLG
    - PYPY
    - PYTH
    - 'PYTH 3.5'
    - RUBY
    - SCALA
    - 'SCM chicken'
    - 'SCM guile'
    - 'SCM qobi'
    - ST
    - TCL
    - TEXT
    - WSPC
max_timelimit: '2'
source_sizelimit: '50000'
problem_author: errichto
problem_tester: null
date_added: 1-05-2017
tags:
    - errichto
    - implementation
    - july17
    - medium
    - simulation
editorial_url: 'https://discuss.codechef.com/problems/MULDIG'
time:
    view_start_date: 1500283800
    submit_start_date: 1500283800
    visible_start_date: 1500283800
    end_date: 1735669800
    current: 1514816033
layout: problem
---
All submissions for this problem are available.###  Read problems statements in [Mandarin Chinese](http://www.codechef.com/download/translated/JULY17/mandarin/MULDIG.pdf), [Russian](http://www.codechef.com/download/translated/JULY17/russian/MULDIG.pdf) and [Vietnamese](http://www.codechef.com/download/translated/JULY17/vietnamese/MULDIG.pdf) as well.

Bear Limak hopes you can solve the following problem. You are given an integer **B** which is equal to 3, 5 or 7. Your goal will be to print a sequence of moves that are able to multiply any two 2-digit numbers X and Y in base **B**.

Consider a computer memory consisting of 105 cells, numbered 0 through 105-1, each storing one digit (in base **B**, a digit must be between 0 and **B** - 1, inclusive). Let ti denote the digit in the i-th cell. Initially:

- ti = i for i B
- t**B** and t**B**+1 are digits of the number X, so X = t**B** \* **B** + t**B**+1
- t**B**+2 and t**B**+3 are digits of the number Y, so Y = t**B+2** \* **B** + t**B**+3
- ti = 0 for all i > **B**+3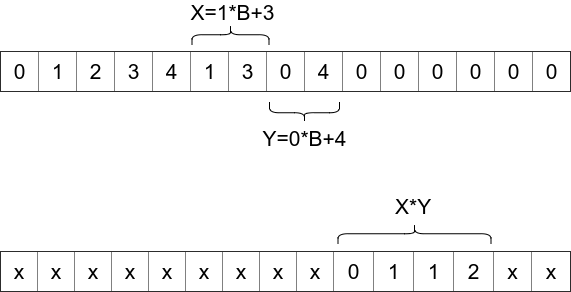

![](https://codechef_shared.s3.amazonaws.com/download/upload/JULY17/a9oimq.jpg)The first of the two drawings above shows the initial situation for **B** = 5 and multiplying numbers 8 and 4 (represented in base 5 as 13 and 04 respectively). After applying your sequence of moves, the result of the multiplication should be stored in cells **B**+4, **B**+5, **B**+6, **B**+7, which is shown in the second drawing (please note that 8 \* 4 = 32 and this number is represented as 0112 in base 5). Except for those 4 cells containing the answer, the final value of ti doesn't matter. In particular, you are allowed to change values in the first **B+4** cells.

You should choose one function F : \[0,**B**-1\] × \[0,**B**-1\] -> \[0,**B**-1\]. It means that the function F should take two digits and return one, where each digit is in the set {0, 1, ..., **B**-1}. One example of F is addition F(x, y) = (x + y) % **B**. We don't require any particular properties from F (e.g. associativity or symmetricity).

You should create a sequence of at most 105 moves. In each move, choose three cells c1, c2 and c3, not necessarily distinct. The result of F for digits in cells c1 and c2 will be computed, and then written in the cell c3. In other words, in C++ or Python it's the operation t\[c3\] = F(t\[c1\], t\[c2\]). For every possible pair of 2-digit numbers X and Y, your sequence of moves should produce the correct answer X \* Y as described above.

### Input

The only line of the input contains a single integer **B**, denoting the base.

### Output

You should first print the description of the function F that you choose, and then the chosen sequence of moves.

First print **B** lines. The i-th line should contain **B** space-separated integers F(i,0), F(i,1), ..., F(i,**B**-1).

In the next line, print a single integer K, denoting the number of moves in the sequence.

In the i-th of the next K lines, print three space-separated integers c1, c2, c3 (each between 0 and 105-1 inclusive), describing the i-th move.

### Subtasks

There are 5 subtasks, each worth 20 points. 1. **B** = 3 and the checker checks only if your program works correctly for X and Y consisting of digits 0 and 1 only (in base **B**).
2. **B** = 3
3. **B** = 5
4. **B** = 5 and the first digit (in base **B**) of X and the first digit of Y are both 0. In other words: X, Y B.
5. **B** = 7
### Example

<pre><b>Input:</b>
3

<b>Output (please note that it's incorrect):</b>
1 1 2
2 2 2
0 1 0
2
1 6 7
0 0 0
</pre>### Explanation

The provided output has valid formatting but isn't correct. Let's analyze the printed moves to multiply X = 7 and Y = 5. These X and Y in base 3 are 21 and 12 respectively, so the initial numbers in cells are: 0, 1, 2, 2, 1, 1, 2, 0, 0, ...

The first operation is t\[7\] = F(t\[1\], t\[6\]) = F(1, 2) = 2, so now we have cells: 0, 1, 2, 2, 1, 1, 2, **2**, 0, ...

The second operation is t\[0\] = F(t\[0\], t\[0\]) = F(0, 0) = 1, so we will have: **1**, 1, 2, 2, 1, 1, 2, 2, 0, ...

After those two operations, cells 7, 8, 9, 10 should contain the product X \* Y = 35, while in fact the contain digits 2, 0, 0, 0, what represents a number 2 \* 33 = 2 \* 27 = 54. The printed sequence of moves should correctly multiply any two 2-digit numbers X, Y, so this particular output would get verdict Wrong Answer.