github.com/captn3m0/codechef.git

---
{"category_name":"medium","problem_code":"SCALSUM","problem_name":"Scalar Product Tree","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{"0":{"id":1,"input":"5 2\r\n5 4 3 2 1\r\n1 2\r\n1 3\r\n2 4\r\n2 5\r\n2 3\r\n4 5","output":"37\r\n43","explanation":"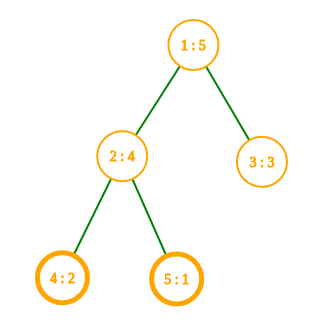![](https://codechef_shared.s3.amazonaws.com/download/Images/NOV20/SCALSUM/SCALSUM.png)\r\n\r\nIn the first query, $F_2 = (4,5)$ and $F_3 = (3,5)$, so the scalar product is $4 \\cdot 3 + 5 \\cdot 5 = 37$.\r\n\r\nIn the second query, $F_4 = (2,4,5)$ and $F_5 = (1,4,5)$, so the scalar product is $2 \\cdot 1 + 4 \\cdot 4 + 5 \\cdot 5 = 43$.","isDeleted":false}}},"video_editorial_url":"https://youtu.be/-n6QKiOtr3w","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":"1 - 3.5","source_sizelimit":50000,"problem_author":"kobor","problem_tester":"","date_added":"17-10-2020","tags":{"0":"kobor","1":"medium","2":"nov20","3":"pre","4":"square","5":"trees"},"problem_difficulty_level":"Medium","best_tag":"Pre Computation","editorial_url":"https://discuss.codechef.com/problems/SCALSUM","time":{"view_start_date":1104528600,"submit_start_date":1104528600,"visible_start_date":1104528600,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=SCALSUM","is_proctored":false,"visitedContests":{},"layout":"problem"}
---
### Read problem statements in [Hindi](https://www.codechef.com/download/translated/NOV20/hindi/SCALSUM.pdf), [Bengali](https://www.codechef.com/download/translated/NOV20/bengali/SCALSUM.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/NOV20/mandarin/SCALSUM.pdf), [Russian](https://www.codechef.com/download/translated/NOV20/russian/SCALSUM.pdf), and [Vietnamese](https://www.codechef.com/download/translated/NOV20/vietnamese/SCALSUM.pdf) as well.

Chef has a tree with $N$ vertices (numbered $1$ through $N$). The tree is rooted at the vertex $1$. For each valid $i$, the weight of the $i$-th vertex is $w_i$.

For a vertex $u$ with depth $d$ (the root has depth $1$), let's denote the sequence of vertices on the path from $u$ to the root by $(v_1, v_2, \ldots, v_d)$, where $v_1 = u$ and $v_d = 1$. Then, let $F_u$ be the vector (i.e. sequence) $(w_{v_1}, w_{v_2}, \ldots, w_{v_d})$, where the $i$-th element is $F_{u, i} = w_{v_i}$ for each valid $i$.

For any two vertices $u$ and $v$ with the same depth $d$, let's define the [dot product](https://en.wikipedia.org/wiki/Dot_product) $F_u \cdot F_v = \sum_{i=1}^d F_{u,i} \cdot F_{v,i}$.

Your task is to answer $Q$ queries. In each query, you are given two vertices $u$ and $v$ with the same depth, and you should find $F_u \cdot F_v$. Since the dot product can be large, compute it modulo $2^{32}$.

### Input
- The first line of the input contains two space-separated integers $N$ and $Q$.
- The second line contains $N$ space-separated integers $w_1, w_2, \ldots, w_N$.
- Each of the next $N-1$ lines contains two space-separated integers $u$ and $v$ denoting that vertices $u$ and $v$ are connected by an edge.
- $Q$ lines follow. Each of these lines contains two space-separated integers $u$ and $v$ describing a query.

### Output
For each query, print a single line containing one integer $F_u \cdot F_v$ modulo $2^{32}$.

### Constraints 
- $1 \le N, Q \le 3 \cdot 10^5$
- $1 \le w_i \le 10^9$ for each valid $i$
- $1 \le u, v \le N$
- in each query, $u$ and $v$ have the same depth

### Subtasks
**Subtask #1 (15 points, time limit 1 second):** $N, Q \le 1,000$

**Subtask #2 (45 points, time limit 2 seconds):** $N, Q \le 10^5$

**Subtask #3 (40 points, time limit 3.5 seconds):** original constraints

### Example Input
```
5 2
5 4 3 2 1
1 2
1 3
2 4
2 5
2 3
4 5
```

### Example Output
```
37
43
```

### Explanation
![](https://codechef_shared.s3.amazonaws.com/download/Images/NOV20/SCALSUM/SCALSUM.png)

In the first query, $F_2 = (4,5)$ and $F_3 = (3,5)$, so the scalar product is $4 \cdot 3 + 5 \cdot 5 = 37$.

In the second query, $F_4 = (2,4,5)$ and $F_5 = (1,4,5)$, so the scalar product is $2 \cdot 1 + 4 \cdot 4 + 5 \cdot 5 = 43$. 

<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>