---{"category_name":"hard","problem_code":"SELEDGE","problem_name":"Selecting Edges","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{"0":{"id":1,"input":"1\r\n5 5 2\r\n1 2 4 8 16\r\n1 2 1\r\n1 3 2\r\n3 4 2\r\n4 5 2\r\n2 5 1","output":27,"explanation":"**Example case 1:**\r\n\r\n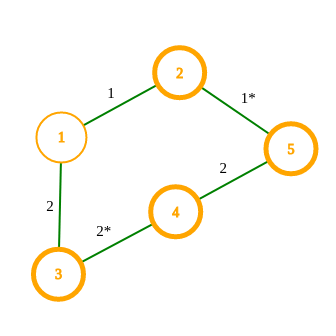\r\n\r\nThe largest value is obtained when $S$ contains only edges $(2, 5)$ and $(3, 4)$. In that case, $V(S)$ contains the vertices $2, 3, 4, 5$.","isDeleted":false}}},"video_editorial_url":"https://youtu.be/gbv40YNe1AY","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":5.678,"source_sizelimit":50000,"problem_author":"ratingoverflow","problem_tester":"","date_added":"13-10-2020","tags":{"0":"depth","1":"flows","2":"hard","3":"min","4":"nov20","5":"randomized","6":"ratingoverflow"},"problem_difficulty_level":"Hard","best_tag":"Depth First Search","editorial_url":"https://discuss.codechef.com/problems/SELEDGE","time":{"view_start_date":1104528600,"submit_start_date":1104528600,"visible_start_date":1104528600,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=SELEDGE","is_proctored":false,"visitedContests":{},"layout":"problem"}---### Read problem statements in [Hindi](https://www.codechef.com/download/translated/NOV20/hindi/SELEDGE.pdf), [Bengali](https://www.codechef.com/download/translated/NOV20/bengali/SELEDGE.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/NOV20/mandarin/SELEDGE.pdf), [Russian](https://www.codechef.com/download/translated/NOV20/russian/SELEDGE.pdf), and [Vietnamese](https://www.codechef.com/download/translated/NOV20/vietnamese/SELEDGE.pdf) as well.You are given an undirected graph $G$ with $N$ vertices (numbered $1$ through $N$) and $M$ edges (numbered $1$ through $M$). $G$ does not contain any self-loops, but it may contain parallel edges. For each valid $i$, the $i$-th vertex has a non-negative integer weight $A_i$. Also, for each valid $i$, the $i$-th edge has a non-negative integer weight $B_i$.Let $E = \{1, 2, \ldots, M\}$ denote the set of edges and for any subset $S \subseteq E$, let $V(S)$ denote the set of vertices which are endpoints of at least one edge from $S$. You should find$$\max\limits_{S\subseteq E, |S| \le K} \left(\sum\limits_{v \in V(S)} A_v - \sum\limits_{e \in S} B_e\right) \,.$$In other words, among all subsets of at most $K$ (but possibly zero) edges, you should find the largest value of the expression "sum of weights of their endpoints, where each endpoint is counted only once, minus the sum of weights of these edges". Note that $S$ may contain multiple parallel edges with the same weights ― they are still considered distinct.### Input- The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows.- The first line of each test case contains three space-separated integers $N$, $M$ and $K$.- The second line contains $N$ space-separated integers $A_1, A_2, \ldots, A_N$.- $M$ lines follow. For each valid $i$, the $i$-th of these lines contains three space-separated integers $u_i$, $v_i$ and $B_i$, describing an edge between vertices $u_i$ and $v_i$ with weight $B_i$.### OutputFor each test case, print a single line containing one integer ― the largest value of the given expression.### Constraints- $T = 5$- $1 \le N, M \le 100$- $1 \le K \le 10$- $0 \le A_i \le 10^8$ for each valid $i$- $0 \le B_i \le 10^8$ for each valid $i$- $1 \le u_i, v_i \le N$ for each valid $i$- $u_i \neq v_i$ for each valid $i$### Subtasks**Subtask #1 (5 points):**- $G$ does not contain any cycles or parallel edges- $K \le 7$**Subtask #2 (15 points):**- $A_i = 1$ for each valid $i$- $B_i = 0$ for each valid $i$- $K \le 7$**Subtask #3 (65 points):** $K \le 9$**Subtask #4 (15 points):** original constraints### Example Input```15 5 21 2 4 8 161 2 11 3 23 4 24 5 22 5 1```### Example Output```27```### Explanation**Example case 1:**The largest value is obtained when $S$ contains only edges $(2, 5)$ and $(3, 4)$. In that case, $V(S)$ contains the vertices $2, 3, 4, 5$.<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>