github.com/captn3m0/codechef.git

---
{"category_name":"hard","problem_code":"RGY","problem_name":"Chef Thanos Wants Perfect Balance","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{}},"video_editorial_url":"","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":5,"source_sizelimit":50000,"problem_author":"mohammed200218","problem_tester":"","date_added":"1-08-2020","tags":{"0":"aug20","1":"daniel_1999","2":"depth","3":"hard","4":"link","5":"matching","6":"mohammed200218","7":"mohammed200218","8":"rishup_nitdgp"},"problem_difficulty_level":"Hard","best_tag":"Depth First Search","editorial_url":"https://discuss.codechef.com/problems/RGY","time":{"view_start_date":1597656602,"submit_start_date":1597656602,"visible_start_date":1597656602,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=RGY","is_proctored":false,"visitedContests":{},"layout":"problem"}
---
### Read problem statements in [Hindi](https://www.codechef.com/download/translated/AUG20/hindi/RGY.pdf), [Bengali](https://www.codechef.com/download/translated/AUG20/bengali/RGY.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/AUG20/mandarin/RGY.pdf), [Russian](https://www.codechef.com/download/translated/AUG20/russian/RGY.pdf), and [Vietnamese](https://www.codechef.com/download/translated/AUG20/vietnamese/RGY.pdf) as well.

Chef Thanos has an undirected simple graph with $N$ vertices (numbered $1$ through $N$) and $M$ edges (numbered $1$ through $M$). For each valid $i$, the $i$-th edge connects vertices $u_i$ and $v_i$. Chef Thanos wants to colour the edges in red and green so that the graph would be perfectly balanced, which means that for each vertex, the number of red edges incident to it must be equal to the number of green edges incident to it.

Obviously, Chef Thanos does not want to leave any edges colourless, but he immediately realised that in such a case, it generally may be impossible to make the graph perfectly balanced, so he decided to colour some of the edges yellow instead, so that it is always possible.

Since Chef Thanos hates the colour yellow, his satisfaction with the graph will be greater when he uses fewer yellow edges. Can you help him choose how to colour the edges so that you remain in the surviving half of humanity?

### Input
- The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows.
- The first line of each test case contains two space-separated integers $N$ and $M$.
- $M$ lines follow. For each valid $i$, the $i$-th of these lines contains two space-separated integers $u_i$ and $v_i$.

### Output
Print $M$ lines. For each valid $i$, the $i$-th of these lines should contain the integer $0$ if you want the $i$-th edge to be yellow, $1$ if you want it to be red or $-1$ if you want it to be green.

### Constraints
- $1 \le N \le 10^5$
- $0 \le M \le 3 \cdot 10^5$
- $1 \le u_i, v_i \le N$ for each valid $i$
- the graph does not contain any self-loops or parallel edges, but it can be disconnected
- the sum of $N$ over all the test cases does not exceed $3 \cdot 10^5$
- the sum of $M$ over all the test cases does not exceed $9 \cdot 10^5$

### Scoring
If your output is invalid or you do not colour the graph in a perfectly balanced way, you will receive the Wrong Answer verdict and 0 points. Otherwise:
- For each test case, let's define $R = Y/N$, where $Y$ is the number of yellow edges you used to colour a graph with $N$ vertices. We then take the maximum of $R$ across all test cases and denote it by $R_{max}$.
- If $R_{max} \ge 3$, you will receive 0 points because you used too many yellow edges (but you will still receive the Accepted verdict).
- If $2 \le R_{max} \lt 3$, you will receive 20 points.
- If $1.5 \le R_{max} \lt 2$, you will receive 40 points.
- If $R_{max} \lt 1.5$, you will receive 100 points.

Note that you do not have to use the smallest number of yellow edges.

### Example Input
```
2
5 6
1 2
2 3
3 1
3 4
4 5
5 3
6 9
1 2
1 3
1 4
2 3
2 4
3 4
3 6
4 5
5 6
```

### Example Output
```
-1
1
1
-1
1
-1
-1
1
0
0
1
-1
0
0
0
```

### Explanation
**Example case 1:** The graph can be perfectly balanced without using any yellow edges.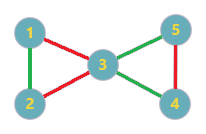

![fig1](https://codechef_shared.s3.amazonaws.com/download/Images/AUG20/RGY/1.png)

**Example case 2:** The first colouring in the figure below corresponds to the output. Note, again, that you do not have to completely minimise the number of yellow edges, so even though the second colouring is also perfectly balanced and uses fewer yellow edges, both of them would receive 100 points.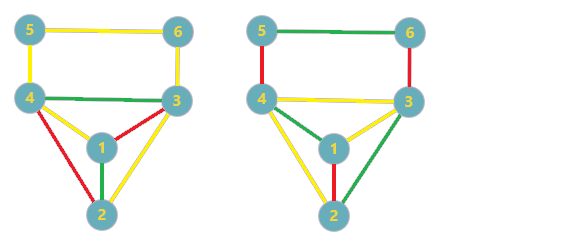

![fig2](https://codechef_shared.s3.amazonaws.com/download/Images/AUG20/RGY/2.png)


<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>