github.com/captn3m0/codechef.git

---
{"category_name":"easy","problem_code":"ACCBIP","problem_name":"Insanely Hard School Exams","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{"0":{"id":1,"input":"2\r\n7 2 13\r\n1 10 1\r\n1 14 2\r\n6 4 1\r\n2 2 1\r\n0 12 2\r\n2 11 2\r\n0 6 1\r\n8 10\r\n6 1 20\r\n1 5 1\r\n2 11 1\r\n4 0 1\r\n6 8 1\r\n0 11 1\r\n3 3 1\r\n9","output":"2\r\n4","explanation":"**Example case 1:** We can remove exactly one line. Initially, we have $5$ truly geometric triangles (see the image below; red is colour $1$ and green is colour $2$).\r\n- Removing any line with colour $2$ brings the total number of truly-geometric triangles down to $4+0=4$.\r\n- Removing any line with colour $1$ brings the total number of truly-geometric triangles down to $1+1=2$.\r\n\r\nThus, the smallest number of truly-geometric triangles we can obtain is $2$.\r\n\r\n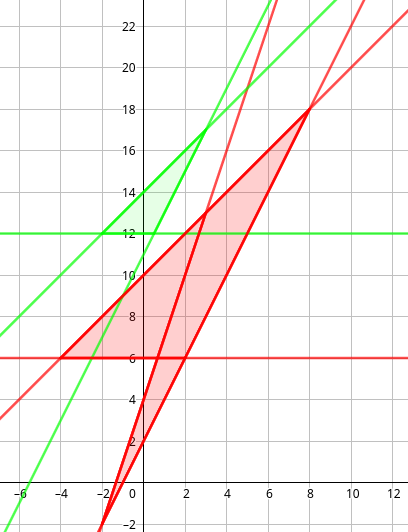![desc](https://codechef_shared.s3.amazonaws.com/download/Images/AUG20/ACCBIP/ACCBIP.png)\r\n\r\n**Example case 2:** We can remove at most $2$ lines and removing any $2$ lines gives us a total of $4$ truly-geometric triangles.","isDeleted":false}}},"video_editorial_url":"","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":1,"source_sizelimit":50000,"problem_author":"infinitepro","problem_tester":"","date_added":"19-04-2020","tags":{"0":"aug20","1":"combinatorics","2":"daniel_1999","3":"dynamic","4":"greedy","5":"infinitepro","6":"infinitepro","7":"medium","8":"rishup_nitdgp"},"problem_difficulty_level":"Medium","best_tag":"Dynamic Programming","editorial_url":"https://discuss.codechef.com/problems/ACCBIP","time":{"view_start_date":1597656602,"submit_start_date":1597656602,"visible_start_date":1597656602,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=ACCBIP","is_proctored":false,"visitedContests":{},"layout":"problem"}
---
### Read problem statements in [Hindi](https://www.codechef.com/download/translated/AUG20/hindi/ACCBIP.pdf), [Bengali](https://www.codechef.com/download/translated/AUG20/bengali/ACCBIP.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/AUG20/mandarin/ACCBIP.pdf), [Russian](https://www.codechef.com/download/translated/AUG20/russian/ACCBIP.pdf), and [Vietnamese](https://www.codechef.com/download/translated/AUG20/vietnamese/ACCBIP.pdf) as well.

After failing to clear his school mathematics examination, infinitepro decided to prepare very hard for his upcoming re-exam, starting with the topic he is weakest at ― computational geometry.

Being an artist, infinitepro has $C$ pencils (numbered $1$ through $C$); each of them draws with one of $C$ distinct colours. He draws $N$ lines (numbered $1$ through $N$) in a 2D Cartesian coordinate system; for each valid $i$, the $i$-th line is drawn with the $c_i$-th pencil and it is described by the equation $y = a_i \cdot x + b_i$.

Now, infinitepro calls a triangle *truly-geometric* if each of its sides is part of some line he drew and all three sides have the same colour. He wants to count these triangles, but there are too many of them! After a lot of consideration, he decided to erase a subset of the $N$ lines he drew. He wants to do it with his eraser, which has length $K$.

Whenever erasing a line with a colour $i$, the length of the eraser decreases by $V_i$. In other words, when the eraser has length $k$ and we use it to erase a line with a colour $i$, the length of the eraser decreases to $k-V_i$; if $k \lt V_i$, it is impossible to erase such a line.

Since infinitepro has to study for the re-exam, he wants to minimise the number of truly-geometric triangles. Can you help him find the minimum possible number of truly-geometric triangles which can be obtained by erasing a subset of the $N$ lines in an optimal way? He promised a grand treat for you if he passes the examination!

### Input
- The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows.
- The first line of the input contains three space-separated integers $N$, $C$ and $K$.
- $N$ lines follow. For each $i$ ($1 \le i \le N$), the $i$-th of these lines contains three space-separated integers $a_i$, $b_i$ and $c_i$.
- The last line contains $C$ space-separated integers $V_1, V_2, \ldots, V_C$.

### Output
For each test case, print a single line containing one integer ― the smallest possible number of truly-geometric triangles after erasing lines.

### Constraints
- $1 \le T \le 10$
- $1 \le C \le N \le 3,000$
- $0 \le K \le 3,000$
- $0 \le a_i, b_i \le 10^9$ for each valid $i$
- $1 \le c_i \le C$ for each valid $i$
- $0 \le V_i \le K$ for each valid $i$
- no two lines coincide, regardless of their colours
- no three lines are concurrent

### Subtasks
**Subtask #1 (10 points):**
- $N \le 10$
- $K \le 100$

**Subtask 2 (15 points):**
- $V_1 = V_2 = \ldots = V_C$
- no two lines are parallel

**Subtask #3 (25 points):** no two lines are parallel

**Subtask #4 (50 points):** original constraints

### Example Input
```
2
7 2 13
1 10 1
1 14 2
6 4 1
2 2 1
0 12 2
2 11 2
0 6 1
8 10
6 1 20
1 5 1
2 11 1
4 0 1
6 8 1
0 11 1
3 3 1
9
```

### Example Output
```
2
4
```

### Explanation
**Example case 1:** We can remove exactly one line. Initially, we have $5$ truly geometric triangles (see the image below; red is colour $1$ and green is colour $2$).
- Removing any line with colour $2$ brings the total number of truly-geometric triangles down to $4+0=4$.
- Removing any line with colour $1$ brings the total number of truly-geometric triangles down to $1+1=2$.

Thus, the smallest number of truly-geometric triangles we can obtain is $2$.

![desc](https://codechef_shared.s3.amazonaws.com/download/Images/AUG20/ACCBIP/ACCBIP.png)

**Example case 2:** We can remove at most $2$ lines and removing any $2$ lines gives us a total of $4$ truly-geometric triangles.

<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>