---{"category_name":"medium","problem_code":"RWALKS","problem_name":"Random Walk Queries","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{"0":{"id":1,"input":"6 4\r\n6 2\r\n3 2\r\n4 1\r\n1 2\r\n5 4\r\n1 6 2\r\n2 4\r\n1 2 3\r\n2 4","output":"500000004\r\n1","explanation":"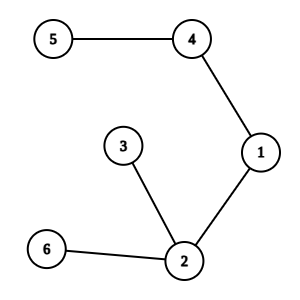\r\n\r\n- For task $1$, all the towns can possibly be visited in the random walk. The probabilities of visiting them are $\\left(1, \\frac{1}{2}, \\frac{1}{4}, \\frac{1}{2}, \\frac{1}{2}, \\frac{1}{4}\\right)$.\r\n- For task $2$, the expected number of times town $5$ would have been visited so far is $\\frac{1}{2}$.\r\n- For task $3$, the probabilities of visiting the towns during this random walk are $\\left(\\frac{1}{2}, 1, 1, \\frac{1}{2}, \\frac{1}{2}, \\frac{1}{2} \\right)$.\r\n- For task $4$, the expected number of times town $5$ would have been visited is $\\frac{1}{2} + \\frac{1}{2} = 1$.","isDeleted":false}}},"video_editorial_url":"","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":"1 - 4","source_sizelimit":50000,"problem_author":"shaanknight","problem_tester":"","date_added":"26-02-2021","tags":{"0":"centroid","1":"lowest","2":"march21","3":"medium","4":"shaanknight","5":"trie"},"problem_difficulty_level":"Medium-Hard","best_tag":"Lowest Common Ancestor","editorial_url":"https://discuss.codechef.com/problems/RWALKS","time":{"view_start_date":1104528600,"submit_start_date":1104528600,"visible_start_date":1104528600,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=RWALKS","is_proctored":false,"visitedContests":{},"layout":"problem"}---### Read problem statements in [Bengali](https://www.codechef.com/download/translated/MARCH21/bengali/RWALKS.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/MARCH21/mandarin/RWALKS.pdf), [Russian](https://www.codechef.com/download/translated/MARCH21/russian/RWALKS.pdf), and [Vietnamese](https://www.codechef.com/download/translated/MARCH21/vietnamese/RWALKS.pdf) as well.Chef visited his native country Chefland for vacation. Chefland has $N$ towns (numbered $1$ through $N$) and $N-1$ bidirectional roads connecting the towns in such a way that it is possible to travel from each town to any other town.Chef had a series of $Q$ tasks he wanted to perform in Chefland. There are two types of tasks:- `1 u d`: Chef should make a random walk with a maximum length $d$, starting from town $u$.- `2 u`: Write down the number of times Chef has visited town $u$ so far.A random walk with the above parameters $(u,d)$ is made in the following way:- First, Chef visits town $u$.- Then, he uniformly randomly chooses a neighbouring town of the town he is currently in (a town directly connected to it by a road), which has not been visited so far, and moves to it (visits it).- If there is no such town or he has already travelled a distance $d$ (visited $d+1$ towns), the walk ends.- Otherwise, Chef continues from step 2 again.However, there is an issue ― Chef quickly forgets the exact paths he has travelled. Hence, he cannot write down exact numbers in tasks of the second type. He would like you to at least tell him, for each task of the second type, the expected value of the number he would write down in this task.Help Chef and find these expected values. Note that Chef's sequence of tasks is encoded so that they have to be processed online. It can be proved that at any point, the expected number of times a city is visited can be expressed as a fraction $\frac{P}{Q}$, where $P$ and $Q$ are non-negative integers and $Q$ is coprime with $10^9+7$. You should compute $P \cdot Q^{-1}$ modulo $10^9+7$, where $Q^{-1}$ denotes the multiplicative inverse of $Q$ modulo $10^9+7$.### Input- The first line of the input contains two space-separated integers $N$ and $Q$.- Each of the next $N-1$ lines contains two space-separated integers $u$ and $v$ denoting that towns $u$ and $v$ are connected by a road.- Each of the next $Q$ lines describes a task as follows:- Let $last$ denote the answer for the last task of the second type so far, or $last = 0$ if there are no such tasks yet.- For a task of the first type, this line contains three space-separated integers $1$, $a$ and $b$. The starting town is decoded as $u = (last + a) \% N + 1$ and the maximum length is decoded as $d = (last + b) \% N + 1$.- For a task of the second type, this line contains two space-separated integers $2$ and $a$. The town $u = (last + a) \% N + 1$.### OutputFor each task of the second type, print a single line containing one integer $P \cdot Q^{-1}$ modulo $10^9+7$.### Constraints- $1 \leq N \leq 2 \cdot 10^5$- $2 \leq Q \leq 10^5$- $1 \leq u,v \leq N$- $1 \leq a,b \leq N$### Subtasks**Subtask #1 (10 points, time limit 1 second):** $N,Q \leq 10^3$**Subtask #2 (25 points, time limit 2 seconds):** $N,Q \leq 5 \cdot 10^4$**Subtask #3 (25 points, time limit 4 seconds):** all towns in Chefland lie on a single straight path**Subtask #4 (40 points, time limit 4 seconds):** original constraints### Example Input```6 46 23 24 11 25 41 6 22 41 2 32 4```### Example Output```5000000041```### Explanation- For task $1$, all the towns can possibly be visited in the random walk. The probabilities of visiting them are $\left(1, \frac{1}{2}, \frac{1}{4}, \frac{1}{2}, \frac{1}{2}, \frac{1}{4}\right)$.- For task $2$, the expected number of times town $5$ would have been visited so far is $\frac{1}{2}$.- For task $3$, the probabilities of visiting the towns during this random walk are $\left(\frac{1}{2}, 1, 1, \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right)$.- For task $4$, the expected number of times town $5$ would have been visited is $\frac{1}{2} + \frac{1}{2} = 1$.<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>