---{"category_name":"medium","problem_code":"MVCN2TST","problem_name":"Move the Coins - Creating Tests","problemComponents":{"constraints":"","constraintsState":false,"subtasks":"","subtasksState":false,"inputFormat":"","inputFormatState":false,"outputFormat":"","outputFormatState":false,"sampleTestCases":{"0":{"id":1,"input":"2\r\n5\r\n1 3\r\n1 2\r\n2 4\r\n2 5\r\n3\r\n5\r\n23\r\n72\r\n7\r\n1 7\r\n2 1\r\n6 1\r\n5 4\r\n3 5\r\n1 5\r\n5\r\n9\r\n6\r\n35\r\n313\r\n602","output":"126\r\n910","explanation":"**Example case 1:** The tree $G$ is\r\n\r\n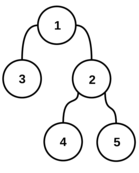\r\n\r\nThere are $25$ reparentings $(u,v)$ ? too many to draw all of them! However, here is a representative sampling. Valid reparentings are marked with a \u0027?\u0027; invalid ones with a \u0027?\u0027:\r\n\r\n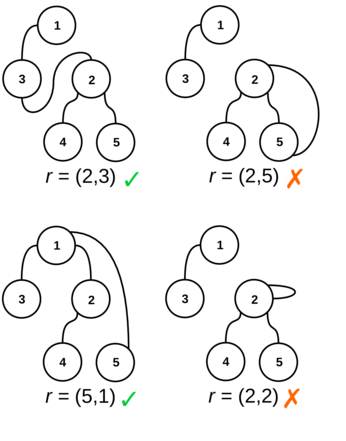\r\n\r\nWe can also form a table of validity of all reparentings $(u,v)$:\r\n```\r\n v\r\n 1 2 3 4 5 \r\n ?????????\r\n 1 ?? ? ? ? ? \r\n 2 ?? ? ? ? ? \r\nu 3 ?? ? ? ? ? \r\n 4 ?? ? ? ? ? \r\n 5 ?? ? ? ? ? \r\n```\r\n\r\nOur initial list $L$, then, is formed by listing all pairs $(u, v)$ with a \u0027?\u0027 and sorting in the order described above. We get the following list:\r\n```\r\n # u v h\r\n 1. 2 1 0\r\n 2. 2 3 1\r\n 3. 3 1 0\r\n 4. 3 2 1\r\n 5. 3 4 2\r\n 6. 3 5 2\r\n 7. 4 1 0\r\n 8. 4 2 1\r\n 9. 4 3 1\r\n10. 4 5 2\r\n11. 5 1 0\r\n12. 5 2 1\r\n13. 5 3 1\r\n14. 5 4 2\r\n```\r\n\r\nFor $i = 1, 2, 3$, we need to decrypt $e_i$ to get $c_i$, then find the corresponding reparenting $(u_i,v_i)$ in the current list $L$, remove it from $L$ and use it to update our decryption key $d$. The initial value of $d$ is $0$. The first encrypted choice is $e_1 = 5$; we decrypt it to get $c_1 = d \\oplus e_1 = 0 \\oplus 5 = 5$, so the reparenting corresponding to the first choice is the $5$-th entry in the current list $L$, which is $(u_1, v_1) = (3, 4)$. We update $d$ to $(0 + 2^1 \\cdot u_1 + 3^1 \\cdot v_1) \\,\\%\\, (10^9+7) = 18$ and remove the $5$-th element from $L$, which becomes\r\n```\r\n # u v h\r\n 1. 2 1 0\r\n 2. 2 3 1\r\n 3. 3 1 0\r\n 4. 3 2 1\r\n 5. 3 5 2\r\n 6. 4 1 0\r\n 7. 4 2 1\r\n 8. 4 3 1\r\n 9. 4 5 2\r\n10. 5 1 0\r\n11. 5 2 1\r\n12. 5 3 1\r\n13. 5 4 2\r\n```\r\n\r\nOn to the second choice! $e_2 = 23$, so $c_2 = 18 \\oplus 23 = 5$ and the reparenting $(u_2, v_2)$ is $(3, 5)$. We update $d$ again to $(18 + 2^2 \\cdot u_2 + 3^2 \\cdot v_2) \\,\\%\\, (10^9+7) = 75$ and remove $(3, 5)$ from our list $L$, which becomes\r\n```\r\n # u v h\r\n 1. 2 1 0\r\n 2. 2 3 1\r\n 3. 3 1 0\r\n 4. 3 2 1\r\n 5. 4 1 0\r\n 6. 4 2 1\r\n 7. 4 3 1\r\n 8. 4 5 2\r\n 9. 5 1 0\r\n10. 5 2 1\r\n11. 5 3 1\r\n12. 5 4 2\r\n```\r\n\r\nOn to the third and final choice! With $e_3 = 72$, we decrypt $c_3 = 75 \\oplus 72 = 3$, so the reparenting $(u_3, v_3) = (3, 1)$. We use this to update $d$ for the final time to $(75 + 2^3 \\cdot u_3 + 3^3 \\cdot v_3) \\,\\%\\, (10^9+7) = 126$.\r\n\r\nWe have now processed all $Q$ choices, and the final decryption key is $d=126$.\r\n\r\n**Example case 2:** The tree $G$ is\r\n\r\n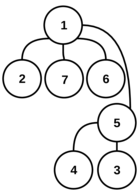\r\n\r\nThere are $49$ possible reparentings; again, we only show a representative sample of them and their validity:\r\n\r\n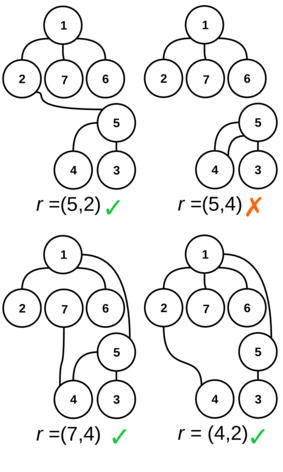\r\n\r\nThe whole table of validity of reparentings is\r\n\r\n```\r\n v\r\n 1 2 3 4 5 6 7 \r\n ?????????????\r\n 1 ?? ? ? ? ? ? ? \r\n 2 ?? ? ? ? ? ? ? \r\n 3 ?? ? ? ? ? ? ? \r\nu 4 ?? ? ? ? ? ? ? \r\n 5 ?? ? ? ? ? ? ? \r\n 6 ?? ? ? ? ? ? ? \r\n 7 ?? ? ? ? ? ? ? \r\n```\r\n\r\nBy listing the valid ones and sorting them in the described order, we get our initial list $L$:\r\n\r\n```\r\n # u v h\r\n 1. 2 1 0\r\n 2. 2 5 1\r\n 3. 2 6 1\r\n 4. 2 7 1\r\n 5. 2 3 2\r\n 6. 2 4 2\r\n 7. 3 1 0\r\n 8. 3 2 1\r\n 9. 3 5 1\r\n10. 3 6 1\r\n11. 3 7 1\r\n12. 3 4 2\r\n13. 4 1 0\r\n14. 4 2 1\r\n15. 4 5 1\r\n16. 4 6 1\r\n17. 4 7 1\r\n18. 4 3 2\r\n19. 5 1 0\r\n20. 5 2 1\r\n21. 5 6 1\r\n22. 5 7 1\r\n23. 6 1 0\r\n24. 6 2 1\r\n25. 6 5 1\r\n26. 6 7 1\r\n27. 6 3 2\r\n28. 6 4 2\r\n29. 7 1 0\r\n30. 7 2 1\r\n31. 7 5 1\r\n32. 7 6 1\r\n33. 7 3 2\r\n34. 7 4 2\r\n```\r\n\r\nThe initial value of $d$ is $0$. The first encrypted value is $e_1 = 9$ and we decrypt it to get $c_1 = d \\oplus e_1 = 0 \\oplus 9 = 9$. The reparenting $(u_1, v_1)$ is the $9$-th element of $L$, i.e. $(u_1, v_1) = (3, 5)$. We update $d$ to $(0 + 2^1 \\cdot u_1 + 3^1 \\cdot v_1) \\,\\%\\, (10^9+7) = 21$ and remove $(3, 5)$ from the list $L$. (To save space, we do not show $L$ after each removal.)\r\n\r\nOn to the next encrypted value $e_2 = 6$: we decrypt it to get $c_2 = 21 \\oplus 6 = 19$, so the reparenting $(u_2, v_2)$ is the $19$-th element of $L$ now (the $20$-th element in the initial list), i.e. $(5, 2)$. We update $d$ to $(21 + 2^2 \\cdot u_2 + 3^2 \\cdot v_2) \\,\\%\\, (10^9+7) = 59$ and remove $(5, 2)$ from $L$.\r\n\r\nNext, $e_3 = 35$, so $c_3 = 59 \\oplus 35 = 24$, $(u_3, v_3) = (6, 7)$, we update $d$ to $(59 + 2^3 \\cdot u_3 + 3^3 \\cdot v_3) \\,\\%\\, (10^9+7) = 296$ and remove $(6, 7)$ from $L$.\r\n\r\nNext, $e_4 = 313$, so $c_4 = 296 \\oplus 313 = 17$, $(u_4, v_4) = (4, 3)$, we update $d$ to $(296 + 2^4 \\cdot u_4 + 3^4 \\cdot v_4) \\,\\%\\, (10^9+7) = 603$ and remove $(4, 3)$ from $L$.\r\n\r\nThe last of Chef\u0027s encrypted choices is $e_5 = 602$, so $c_5 = 603 \\oplus 602 = 1$, $(u_5, v_5) = (2, 1)$. We update $d$ to $(603 + 2^5 \\cdot u_5 + 3^5 \\cdot v_5) \\,\\%\\, (10^9+7) = 910$.\r\n\r\nWe have now processed all $Q$ of Chef\u0027s choices, and the final decryption key is $d = 910$.","isDeleted":false}}},"video_editorial_url":"","languages_supported":{"0":"CPP14","1":"C","2":"JAVA","3":"PYTH 3.6","4":"CPP17","5":"PYTH","6":"PYP3","7":"CS2","8":"ADA","9":"PYPY","10":"TEXT","11":"PAS fpc","12":"NODEJS","13":"RUBY","14":"PHP","15":"GO","16":"HASK","17":"TCL","18":"PERL","19":"SCALA","20":"LUA","21":"kotlin","22":"BASH","23":"JS","24":"LISP sbcl","25":"rust","26":"PAS gpc","27":"BF","28":"CLOJ","29":"R","30":"D","31":"CAML","32":"FORT","33":"ASM","34":"swift","35":"FS","36":"WSPC","37":"LISP clisp","38":"SQL","39":"SCM guile","40":"PERL6","41":"ERL","42":"CLPS","43":"ICK","44":"NICE","45":"PRLG","46":"ICON","47":"COB","48":"SCM chicken","49":"PIKE","50":"SCM qobi","51":"ST","52":"SQLQ","53":"NEM"},"max_timelimit":3,"source_sizelimit":50000,"problem_author":"ssjgz","problem_tester":"","date_added":"30-07-2020","tags":{"0":"avl","1":"binary","2":"medium","3":"persistence","4":"persistent","5":"prefix","6":"sept20","7":"ssjgz","8":"ssjgz"},"problem_difficulty_level":"Medium-Hard","best_tag":"Binary Search","editorial_url":"https://discuss.codechef.com/problems/MVCN2TST","time":{"view_start_date":1600075802,"submit_start_date":1600075802,"visible_start_date":1600075802,"end_date":1735669800},"is_direct_submittable":false,"problemDiscussURL":"https://discuss.codechef.com/search?q=MVCN2TST","is_proctored":false,"visitedContests":{},"layout":"problem"}---### Read problem statements in [Hindi](https://www.codechef.com/download/translated/SEPT20/hindi/MVCN2TST.pdf), [Bengali](https://www.codechef.com/download/translated/SEPT20/bengali/MVCN2TST.pdf), [Mandarin Chinese](https://www.codechef.com/download/translated/SEPT20/mandarin/MVCN2TST.pdf), [Russian](https://www.codechef.com/download/translated/SEPT20/russian/MVCN2TST.pdf), and [Vietnamese](https://www.codechef.com/download/translated/SEPT20/vietnamese/MVCN2TST.pdf) as well.Chef is preparing tests for the problem ["Move the Coins"](https://www.hackerrank.com/challenges/move-the-coins/problem)!He needs to create a tree $G$ with $N$ nodes (numbered $1$ through $N$), which is rooted at node $1$, and a list of $Q$ distinct *reparentings*. A reparenting is a pair of nodes $(u, v)$ ($u \neq 1$) of $G$ and the result of applying it to $G$ is another graph, formed as follows:- Take a copy of the original tree $G$.- In this copy, remove the edge connecting the vertex $u$ to its parent.- Then, add a new edge between the nodes $u$ and $v$.As an example, consider the following tree $G$:We wish to apply the reparenting $r = (6, 3)$ to it. The resulting graph would beA reparenting $r$ is *valid* if the resulting graph is still a tree (that is, a connected graph without cycles). For the time being, Chef wants to generate only valid reparentings.Chef has already decided on the tree $G$ and now he just needs to pick $Q$ valid reparentings. He makes an initial list $L$ of all valid reparentings for this tree and sorts them in a special order.Let $r = (u, v)$ and $r' = (u', v')$ be valid reparentings. Their order is decided as follows:- if $u \lt u'$, then $r \lt r'$- if $u \gt u'$, then $r \gt r'$- if $u = u'$, find the distances of nodes $v$ and $v'$ from the root and denote them by $h$ and $h'$ respectively- if $u = u'$ and $h \lt h'$, then $r \lt r'$- if $u = u'$ and $h \gt h'$, then $r \gt r'$- if $u = u'$, $h = h'$ and $v \lt v'$, then $r \lt r'$- if $u = u'$, $h = h'$ and $v \gt v'$, then $r \gt r'$Chef chooses $Q$ integers $c_1, c_2, \ldots, c_Q$, removes the $c_1$-th element of $L$, then removes the $c_2$-th element of the resulting (smaller) list $L$, and so on, until he removes the $c_Q$-th element. The sequence $c_1, c_2, \ldots, c_Q$ is chosen in such a way that during this process, each of them is a valid index of an element in the current list $L$. This way, he removes $Q$ distinct valid reparentings and uses them in one test.Because Chef does not believe in making life easy for himself, the sequence $c_1, c_2, \ldots, c_Q$ is encrypted and each of its elements cannot be decrypted until all previous reparentings are found. More formally, consider a decryption key $d$; initially, $d = 0$. You are given an encrypted sequence $e_1, e_2, \ldots, e_Q$. For each integer $i$ from $1$ to $Q$, Chef decrypts $c_i = e_i \oplus d$ ($\oplus$ denotes the bitwise XOR operator), finds the $c_i$-th reparenting in the current list $L$, denoted by $(u_i, v_i)$, removes it from $L$ and updates the decryption key $d$ to $(d + 2^i \cdot u_i + 3^i \cdot v_i) \,\%\, (10^9+7)$.Can you help Chef find the $Q$ valid reparentings corresponding to his encrypted choices? Calculating the final value of $d$ will suffice to show that you can do it!### Input- The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows.- The first line of each test case contains a single integer $N$.- Each of the next $N-1$ lines contains two space-separated integers $a$ and $b$ denoting that nodes $a$ and $b$ are connected by an edge.- The next line contains a single integer $Q$.- $Q$ lines follow. For each valid $i$, the $i$-th of these lines contains a single integer $e_i$.### OutputFor each test case, print a single line containing one integer ― the final value of $d$ after processing all $Q$ reparentings.### Constraints- $1 \le T \le 1,000$- $1 \le N, Q \le 200,000$- $1 \le a, b \le N$- $0 \le e_i \le 2^{36}$ for each valid $i$- $1 \le c_i \le R+1-i$ for each valid $i$, where $R$ is the number of valid reparentings- the sum of $N$ over all test cases does not exceed $200,000$- the sum of $Q$ over all test cases does not exceed $200,000$### Subtasks**Subtask #1 (5 points):**- $T \le 10$- $N, Q \le 100$**Subtask #2 (10 points)**:- $T \le 100$- $N, Q \le 1,000$**Subtask #3 (85 points)**: original constraints### Example Input```251 31 22 42 535237271 72 16 15 43 51 559635313602```### Example Output```126910```### Explanation**Example case 1:** The tree $G$ isThere are $25$ reparentings $(u,v)$ ― too many to draw all of them! However, here is a representative sampling. Valid reparentings are marked with a '✓'; invalid ones with a '✗':We can also form a table of validity of all reparentings $(u,v)$:```v1 2 3 4 5─────────1 │✗ ✗ ✗ ✗ ✗2 │✓ ✗ ✓ ✗ ✗u 3 │✓ ✓ ✗ ✓ ✓4 │✓ ✓ ✓ ✗ ✓5 │✓ ✓ ✓ ✓ ✗```Our initial list $L$, then, is formed by listing all pairs $(u, v)$ with a '✓' and sorting in the order described above. We get the following list:```# u v h1. 2 1 02. 2 3 13. 3 1 04. 3 2 15. 3 4 26. 3 5 27. 4 1 08. 4 2 19. 4 3 110. 4 5 211. 5 1 012. 5 2 113. 5 3 114. 5 4 2```For $i = 1, 2, 3$, we need to decrypt $e_i$ to get $c_i$, then find the corresponding reparenting $(u_i,v_i)$ in the current list $L$, remove it from $L$ and use it to update our decryption key $d$. The initial value of $d$ is $0$. The first encrypted choice is $e_1 = 5$; we decrypt it to get $c_1 = d \oplus e_1 = 0 \oplus 5 = 5$, so the reparenting corresponding to the first choice is the $5$-th entry in the current list $L$, which is $(u_1, v_1) = (3, 4)$. We update $d$ to $(0 + 2^1 \cdot u_1 + 3^1 \cdot v_1) \,\%\, (10^9+7) = 18$ and remove the $5$-th element from $L$, which becomes```# u v h1. 2 1 02. 2 3 13. 3 1 04. 3 2 15. 3 5 26. 4 1 07. 4 2 18. 4 3 19. 4 5 210. 5 1 011. 5 2 112. 5 3 113. 5 4 2```On to the second choice! $e_2 = 23$, so $c_2 = 18 \oplus 23 = 5$ and the reparenting $(u_2, v_2)$ is $(3, 5)$. We update $d$ again to $(18 + 2^2 \cdot u_2 + 3^2 \cdot v_2) \,\%\, (10^9+7) = 75$ and remove $(3, 5)$ from our list $L$, which becomes```# u v h1. 2 1 02. 2 3 13. 3 1 04. 3 2 15. 4 1 06. 4 2 17. 4 3 18. 4 5 29. 5 1 010. 5 2 111. 5 3 112. 5 4 2```On to the third and final choice! With $e_3 = 72$, we decrypt $c_3 = 75 \oplus 72 = 3$, so the reparenting $(u_3, v_3) = (3, 1)$. We use this to update $d$ for the final time to $(75 + 2^3 \cdot u_3 + 3^3 \cdot v_3) \,\%\, (10^9+7) = 126$.We have now processed all $Q$ choices, and the final decryption key is $d=126$.**Example case 2:** The tree $G$ isThere are $49$ possible reparentings; again, we only show a representative sample of them and their validity:The whole table of validity of reparentings is```v1 2 3 4 5 6 7─────────────1 │✗ ✗ ✗ ✗ ✗ ✗ ✗2 │✓ ✗ ✓ ✓ ✓ ✓ ✓3 │✓ ✓ ✗ ✓ ✓ ✓ ✓u 4 │✓ ✓ ✓ ✗ ✓ ✓ ✓5 │✓ ✓ ✗ ✗ ✗ ✓ ✓6 │✓ ✓ ✓ ✓ ✓ ✗ ✓7 │✓ ✓ ✓ ✓ ✓ ✓ ✗```By listing the valid ones and sorting them in the described order, we get our initial list $L$:```# u v h1. 2 1 02. 2 5 13. 2 6 14. 2 7 15. 2 3 26. 2 4 27. 3 1 08. 3 2 19. 3 5 110. 3 6 111. 3 7 112. 3 4 213. 4 1 014. 4 2 115. 4 5 116. 4 6 117. 4 7 118. 4 3 219. 5 1 020. 5 2 121. 5 6 122. 5 7 123. 6 1 024. 6 2 125. 6 5 126. 6 7 127. 6 3 228. 6 4 229. 7 1 030. 7 2 131. 7 5 132. 7 6 133. 7 3 234. 7 4 2```The initial value of $d$ is $0$. The first encrypted value is $e_1 = 9$ and we decrypt it to get $c_1 = d \oplus e_1 = 0 \oplus 9 = 9$. The reparenting $(u_1, v_1)$ is the $9$-th element of $L$, i.e. $(u_1, v_1) = (3, 5)$. We update $d$ to $(0 + 2^1 \cdot u_1 + 3^1 \cdot v_1) \,\%\, (10^9+7) = 21$ and remove $(3, 5)$ from the list $L$. (To save space, we do not show $L$ after each removal.)On to the next encrypted value $e_2 = 6$: we decrypt it to get $c_2 = 21 \oplus 6 = 19$, so the reparenting $(u_2, v_2)$ is the $19$-th element of $L$ now (the $20$-th element in the initial list), i.e. $(5, 2)$. We update $d$ to $(21 + 2^2 \cdot u_2 + 3^2 \cdot v_2) \,\%\, (10^9+7) = 59$ and remove $(5, 2)$ from $L$.Next, $e_3 = 35$, so $c_3 = 59 \oplus 35 = 24$, $(u_3, v_3) = (6, 7)$, we update $d$ to $(59 + 2^3 \cdot u_3 + 3^3 \cdot v_3) \,\%\, (10^9+7) = 296$ and remove $(6, 7)$ from $L$.Next, $e_4 = 313$, so $c_4 = 296 \oplus 313 = 17$, $(u_4, v_4) = (4, 3)$, we update $d$ to $(296 + 2^4 \cdot u_4 + 3^4 \cdot v_4) \,\%\, (10^9+7) = 603$ and remove $(4, 3)$ from $L$.The last of Chef's encrypted choices is $e_5 = 602$, so $c_5 = 603 \oplus 602 = 1$, $(u_5, v_5) = (2, 1)$. We update $d$ to $(603 + 2^5 \cdot u_5 + 3^5 \cdot v_5) \,\%\, (10^9+7) = 910$.We have now processed all $Q$ of Chef's choices, and the final decryption key is $d = 910$.<aside style='background: #f8f8f8;padding: 10px 15px;'><div>All submissions for this problem are available.</div></aside>