hn-classics/_stories/2010/9694372.md

created_at	title	url	author	points	story_text	comment_text	num_comments	story_id	story_title	story_url	parent_id	created_at_i	_tags	objectID	year
2015-06-10T18:37:31.000Z	Levenshtein Automata (2010)	http://blog.notdot.net/2010/07/Damn-Cool-Algorithms-Levenshtein-Automata	beau	61			34					1433961451	story author_beau story_9694372	9694372	2010

Source

Damn Cool Algorithms: Levenshtein Automata - Nick's Blog

Nick's Blog

because repeating myself sucks

• Home
• Archive

Search:

Damn Cool Algorithms: Levenshtein Automata

Posted by Nick Johnson | Filed under python, tech, coding, damn-cool-algorithms

In a previous Damn Cool Algorithms post, I talked about BK-trees, a clever indexing structure that makes it possible to search for fuzzy matches on a text string based on Levenshtein distance - or any other metric that obeys the triangle inequality. Today, I'm going to describe an alternative approach, which makes it possible to do fuzzy text search in a regular index: Levenshtein automata.

Introduction

The basic insight behind Levenshtein automata is that it's possible to construct a Finite state automaton that recognizes exactly the set of strings within a given Levenshtein distance of a target word. We can then feed in any word, and the automaton will accept or reject it based on whether the Levenshtein distance to the target word is at most the distance specified when we constructed the automaton. Further, due to the nature of FSAs, it will do so in O(n) time with the length of the string being tested. Compare this to the standard Dynamic Programming Levenshtein algorithm, which takes O(mn) time, where m and n are the lengths of the two input words! It's thus immediately apparrent that Levenshtein automaton provide, at a minimum, a faster way for us to check many words against a single target word and maximum distance - not a bad improvement to start with!

Of course, if that were the only benefit of Levenshtein automata, this would be a short article. There's much more to come, but first let's see what a Levenshtein automaton looks like, and how we can build one.

Construction and evaluation

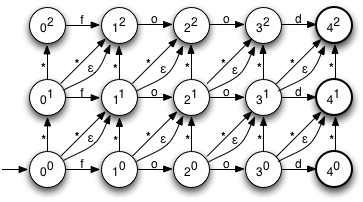
The diagram on the right shows the NFA for a Levenshtein automaton for the word 'food', with maximum edit distance 2. As you can see, it's very regular, and the construction is fairly straightforward. The start state is in the lower left. States are named using a ne style notation, where n is the number of characters consumed so far, and e is the number of errors. Horizontal transitions represent unmodified characters, vertical transitions represent insertions, and the two types of diagonal transitions represent substitutions (the ones marked with a *) and deletions, respectively.

Let's see how we can construct an NFA such as this given an input word and a maximum edit distance. I won't include the source for the NFA class here, since it's fairly standard; for gory details, see the Gist. Here's the relevant function in Python:

def levenshtein_automata(term, k):
  nfa = NFA((0, 0))
  for i, c in enumerate(term):
    for e in range(k + 1):
      # Correct character
      nfa.add_transition((i, e), c, (i + 1, e))
      if e < k:
        # Deletion
        nfa.add_transition((i, e), NFA.ANY, (i, e + 1))
        # Insertion
        nfa.add_transition((i, e), NFA.EPSILON, (i + 1, e + 1))
        # Substitution
        nfa.add_transition((i, e), NFA.ANY, (i + 1, e + 1))
  for e in range(k + 1):
    if e < k:
      nfa.add_transition((len(term), e), NFA.ANY, (len(term), e + 1))
    nfa.add_final_state((len(term), e))
  return nfa

This should be easy to follow; we're basically constructing the transitions you see in the diagram in the most straightforward manner possible, as well as denoting the correct set of final states. State labels are tuples, rather than strings, with the tuples using the same notation we described above.

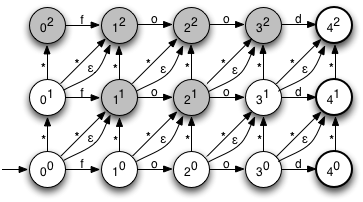
Because this is an NFA, there can be multiple active states. Between them, these represent the possible interpretations of the string processed so far. For example, consider the active states after consuming the characters 'f' and 'x':

This indicates there are several possible variations that are consistent with the first two characters 'f' and 'x': A single substitution, as in 'fxod', a single insertion, as in 'fxood', two insertions, as in 'fxfood', or a substitution and a deletion, as in 'fxd'. Also included are several redundant hypotheses, such as a deletion and an insertion, also resulting in 'fxod'. As more characters are processed, some of these possibilities will be eliminated, while other new ones will be introduced. If, after consuming all the characters in the word, an accepting (bolded) state is in the set of current states, there's a way to convert the input word into the target word with two or fewer changes, and we know we can accept the word as valid.

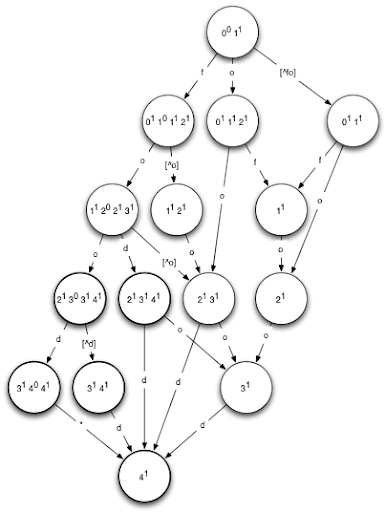
Actually evaluating an NFA directly tends to be fairly computationally expensive, due to the presence of multiple active states, and epsilon transitions (that is, transitions that require no input symbol), so the standard practice is to first convert the NFA to a DFA using powerset construction. Using this algorithm, a DFA is constructed in which each state corresponds to a set of active states in the original NFA. We won't go into detail about powerset construction here, since it's tangential to the main topic. Here's an example of a DFA corresponding to the NFA for the input word 'food' with one allowable error:

Note that we depicted a DFA for one error, as the DFA corresponding to our NFA above is a bit too complex to fit comfortably in a blog post! The DFA above will accept exactly the words that have an edit distance to the word 'food' of 1 or less. Try it out: pick any word, and trace its path through the DFA. If you end up in a bolded state, the word is valid.

I won't include the source for powerset construction here; it's also in the gist for those who care.

Briefly returning to the issue of runtime efficiency, you may be wondering how efficient Levenshtein DFA construction is. We can construct the NFA in O(kn) time, where k is the edit distance and n is the length of the target word. Conversion to a DFA has a worst case of O(2n) time - which leads to a pretty extreme worst-case of O(2kn) runtime! Not all is doom and gloom, though, for two reasons: First of all, Levenshtein automata won't come anywhere near the 2n worst-case for DFA construction*. Second, some very clever computer scientists have come up with algorithms to construct the DFA directly in O(n) time, [SCHULZ2002FAST] and even a method to skip the DFA construction entirely and use a table-based evaluation method!

Indexing

Now that we've established that it's possible to construct Levenshtein automata, and demonstrated how they work, let's take a look at how we can use them to search an index for fuzzy matches efficiently. The first insight, and the approach many papers [SCHULZ2002FAST] [MIHOV2004FAST] take is to observe that a dictionary - that is, the set of records you want to search - can itself be represented as a DFA. In fact, they're frequently stored as a Trie or a DAWG, both of which can be viewed as special cases of DFAs. Given that both the dictionary and the criteria (the Levenshtein automata) are represented as DFAs, it's then possible to efficiently intersect the two DFAs to find exactly the words in the dictionary that match our criteria, using a very simple procedure that looks something like this:

def intersect(dfa1, dfa2):
  stack = [("", dfa1.start_state, dfa2.start_state)]
  while stack:
    s, state1, state2 = stack.pop()
    for edge in set(dfa1.edges(state1)).intersect(dfa2.edges(state2)):
      state1 = dfa1.next(state1, edge)
      state2 = dfa2.next(state2, edge)
      if state1 and state2:
        s = s + edge
        stack.append((s, state1, state2))
        if dfa1.is_final(state1) and dfa2.is_final(state2):
          yield s

That is, we traverse both DFAs in lockstep, only following edges that both DFAs have in common, and keeping track of the path we've followed so far. Any time both DFAs are in a final state, that word is in the output set, so we output it.

This is all very well if your index is stored as a DFA (or a trie or DAWG), but many indexes aren't: if they're in-memory, they're probably in a sorted list, and if they're on disk, they're probably in a BTree or similar structure. Is there a way we can modify this scheme to work with these sort of indexes, and still provide a speedup on brute-force approaches? It turns out that there is.

The critical insight here is that with our criteria expressed as a DFA, we can, given an input string that doesn't match, find the next string (lexicographically speaking) that does. Intuitively, this is fairly easy to do: we evaluate the input string against the DFA until we cannot proceed further - for example, because there's no valid transition for the next character. Then, we repeatedly follow the edge that has the lexicographically smallest label until we reach a final state. Two special cases apply here: First, on the first transition, we need to follow the lexicographically smallest label greater than character that had no valid transition in the preliminary step. Second, if we reach a state with no valid outwards edge, we should backtrack to the previous state, and try again. This is pretty much the 'wall following' maze solving algorithm, as applied to a DFA.

For an example of this, take a look at the DFA for food(1), above, and consider the input word 'foogle'. We consume the first four characters fine, leaving us in state 3141. The only out edge from here is 'd', while the next character is 'l', so we backtrack one step to the previous state, 21303141. From here, our next character is 'g', and there's an out-edge for 'f', so we take that edge, leaving us in an accepting state (the same state as previously, in fact, but with a different path to it) with the output string 'fooh' - the lexicographically next string in the DFA after 'foogle'.

Here's the Python code for it, as a method on the DFA class. As previously, I haven't included boilerplate for the DFA, which is all [here][24].

  def next_valid_string(self, input):
    state = self.start_state
    stack = []
    
    # Evaluate the DFA as far as possible
    for i, x in enumerate(input):
      stack.append((input[:i], state, x))
      state = self.next_state(state, x)
      if not state: break
    else:
      stack.append((input[:i+1], state, None))

    if self.is_final(state):
      # Input word is already valid
      return input
    
    # Perform a 'wall following' search for the lexicographically smallest
    # accepting state.
    while stack:
      path, state, x = stack.pop()
      x = self.find_next_edge(state, x)
      if x:
        path += x
        state = self.next_state(state, x)
        if self.is_final(state):
          return path
        stack.append((path, state, None))
    return None

In the first part of the function, we evaluate the DFA in the normal fashion, keeping a stack of visited states, along with the path so far and the edge we intend to attempt to follow out of them. Then, assuming we didn't find an exact match, we perform the backtracking search we described above, attempting to find the smallest set of transitions we can follow to come to an accepting state. For some caveats about the generality of this function, read on...

Also needed is the utility function find_next_edge, which finds the lexicographically smallest outwards edge from a state that's greater than some given input:

  def find_next_edge(self, s, x):
    if x is None:
      x = u'

[24]: