hn-classics/_stories/2007/11959230.md

---
created_at: '2016-06-23T06:33:08.000Z'
title: The Rule of 72 (2007)
url: http://betterexplained.com/articles/the-rule-of-72/
author: shubhamjain
points: 323
story_text: 
comment_text: 
num_comments: 92
story_id: 
story_title: 
story_url: 
parent_id: 
created_at_i: 1466663588
_tags:
- story
- author_shubhamjain
- story_11959230
objectID: '11959230'
year: 2007

---
The Rule of 72 is a great [mental math
shortcut](https://betterexplained.com/articles/mental-math-shortcuts/)
to estimate the effect of any growth rate, from quick financial
calculations to population estimates. Here’s the formula:

    Years to double = 72 / Interest Rate

This formula is useful for **financial estimates** and understanding the
nature of compound interest. Examples:

  - At 6% interest, your money takes 72/6 or 12 years to double.

  - To double your money in 10 years, get an interest rate of 72/10 or
    7.2%.

  - If your country’s
    
    GDP
    
    grows at 3% a year, the economy doubles in 72/3 or 24 years.

  - If your growth slips to 2%, it will double in 36 years. If growth
    increases to 4%, the economy doubles in 18 years. Given the speed at
    which technology develops, shaving years off your growth time could
    be very important.

You can also use the rule of 72 for **expenses like inflation or
interest**:

  - If inflation rates go from 2% to 3%, your money will lose half its
    value in 24 years instead of 36.
  - If college tuition increases at 5% per year (which is faster than
    inflation), tuition costs will double in 72/5 or about 14.4 years.
    If you pay 15% interest on your credit cards, the amount you owe
    will **double** in only 72/15 or 4.8 years\!

The rule of 72 shows why a “small” 1% difference in inflation or GDP
expansion has a huge effect in forecasting models.

By the way, the Rule of 72 applies to anything that grows, including
population. Can you see why a population growth rate of 3% vs 2% could
be a huge problem for planning? Instead of needing to double your
capacity in 36 years, you only have 24. Twelve years were shaved off
your schedule with one percentage point.

## Deriving the Formula

Half the fun in using this magic formula is seeing how it’s made. Our
goal is to figure out how long it takes for some money (or something
else) to double at a certain interest rate.

Let’s start with $1 since it’s easy to work with (the exact value
doesn’t matter). So, suppose we have $1 and a yearly interest rate R.
After one year we have:

`1 * (1+R)`

For example, at 10% interest, we’d have $1 \* (1 + 0.1) = $1.10 at the
end of the year. After 2 years, we’d have

`1 * (1+R) * (1+R) = 1 * (1+R)^2`

And at 10% interest, we have $1 \* (1.1)2 = $1.21 at the end of year 2.
Notice how the dime we earned the first year starts earning money on its
own (a penny). Next year we create another dime that starts making
pennies for us, along with the small amount the first penny contributes.
As Ben Franklin said: “The money that money earns, earns money”, or “The
dime the dollar earned, earns a penny.” Cool, huh?

This deceptively small, cumulative growth makes compound interest
extremely powerful – Einstein called it one of the most powerful forces
in the universe.

Extending this year after year, after N years we have

`1 * (1+R)^N`

Now, we need to find how long it takes to double — that is, get to 2
dollars. The equation becomes:

`1 * (1+R)^N = 2`

Basically: How many years at R% interest does it take to get to 2? Not
too hard, right? Let’s get to work on this sucka and find N:

    1: 1 * (1+R)^N = 2
    2: (1+R)^N = 2
    3: ln( (1+R)^N ) = ln(2) [natural log of both sides]
    4: N * ln(1+R) = .693
    5: N * R = .693 [For small R, ln(1+R) ~ R]
    6: N = .693 / R

There’s a little trickery on line 5. We use an approximation to say that
ln(1+R) = R. It’s pretty close – even at R = .25 the approximation is
10% accurate ([check accuracy here](http://instacalc.com/22281)). As you
use bigger rates, the accuracy will get worse.

Now let’s clean up the formula a bit. We want to use R as an integer (3)
rather than a decimal (.03), so we multiply the right hand side by 100:

`N = 69.3 / R`

There’s one last step: 69.3 is nice and all, but not easily divisible.
72 is closeby, and has many more factors (2, 3, 4, 6, 12…). So the rule
of 72 it is. Sorry 69.3, we hardly knew ye. (We could use 70, but again,
72 is nearby and even more divisible; for a mental shortcut, go with the
number easiest to divide.)

## Extra Credit

Derive a similar rule for tripling your money – just start with

`1 * (1+R)^N = 3`

Give it a go – if you get stuck, [see the rule of 72 for any
factor](http://instacalc.com/22282).

Happy math.

## A Note On Accuracy

From Colin’s [comment](https://news.ycombinator.com/item?id=11959464) on
Hacker News, the Rule of 72 works because it’s on the “right side” of
`100*ln(2)`.

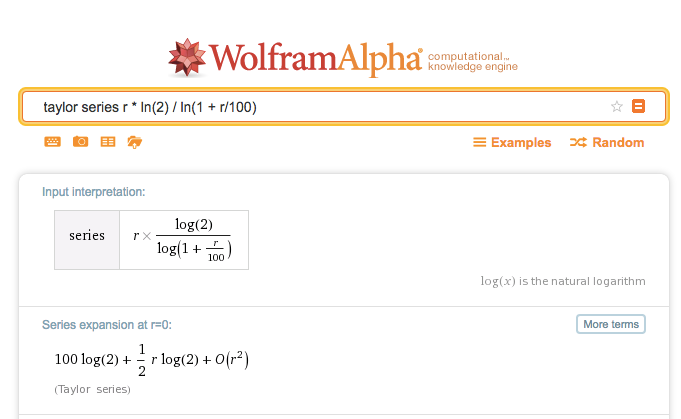
`100*ln(2)` is ~69.3, and 72 rounds up to the bigger side. This is a
great choice because the [series
expansion](https://www.wolframalpha.com/input/?i=taylor+series+ln\(2\)+%2F+ln\(1+%2B+x\))
of `r * ln(2) / ln(1 + r/100)`
is:

![taylor\_series\_r\_\_\_ln\_2\_\_\_\_ln\_1\_\_\_r\_100\_\_-\_Wolfram\_Alpha](https://betterexplained.com/wp-content/uploads/2007/01/taylor_series_r___ln_2____ln_1___r_100__-_Wolfram_Alpha.png)

This series expansion is the Calculus Way of showing how far the initial
estimate strays from the actual result. The first correction term
frac(1)(2) r log(2) is small but grows with r. 72 is on the “right side”
because it helps us stay in the accurate zone for longer. Neat insight\!

## Other Posts In This Series